改訂新版 世界大百科事典 「楕円関数」の意味・わかりやすい解説
楕円関数 (だえんかんすう)
elliptic function
複素平面Cで有理型な二重周期関数の別名である。すなわち,ω1とω2を,0と異なる複素数でIm(ω1/ω2)>0を満たすものとしたとき,Cで有理型な関数fで,任意のz∈Cと,任意の整数m,nに対して,
f(z+2mω1+2nω2)=f(z)
を満たすものを,2ω1と2ω2を基本周期とする楕円関数という(ω1,ω2を採らず2ω1,2ω2を用いるのは,種々の利点があり,慣用となっている)。4点0,2ω1,2ω2,2ω1+2ω2を頂点とする平行四辺形を基本周期平行四辺形という。
歴史的には,楕円関数の研究は,楕円積分に源をもつ。積分,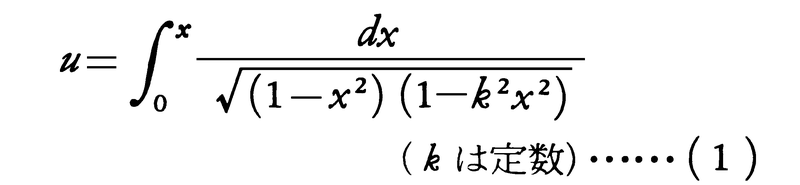
のように の有理関数の積分のことを楕円積分という(楕円の周長を求める際に現れるのでこの名がついた)。この積分の研究は,18世紀から19世紀にかけてL.オイラー,A.ルジャンドルらによって研究されてきた。なお,後者は今日の慣用と異なって楕円積分のことを楕円関数と呼んだ。
の有理関数の積分のことを楕円積分という(楕円の周長を求める際に現れるのでこの名がついた)。この積分の研究は,18世紀から19世紀にかけてL.オイラー,A.ルジャンドルらによって研究されてきた。なお,後者は今日の慣用と異なって楕円積分のことを楕円関数と呼んだ。
楕円積分の研究に革命を与えたのは,19世紀初期のN.アーベルとC.ヤコビである。それは楕円積分u=u(x)の逆関数x=x(u)を考えるという発想であった。ちょうど,
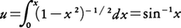 の逆関数がx=sinuであるように,ヤコビは(1)式の逆関数をx=snuと表して,新しい関数を導入した。同様にcnu,dnuを導入し,複素関数として扱い,これらの二重周期性や加法公式,
の逆関数がx=sinuであるように,ヤコビは(1)式の逆関数をx=snuと表して,新しい関数を導入した。同様にcnu,dnuを導入し,複素関数として扱い,これらの二重周期性や加法公式,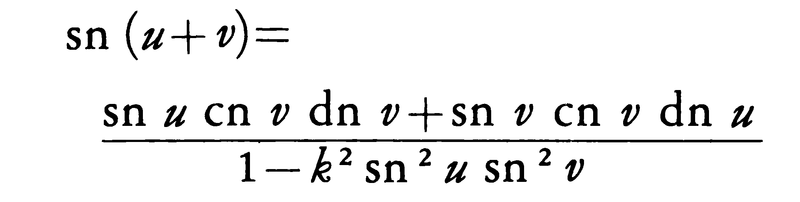
を証明した。
やや遅れて,K.ワイヤーシュトラスはペー関数,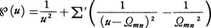 (ただしΩmn=2mω1+2nω2で,Σ′はすべての(m,n)≠(0,0)に対する和)を導入した。これは基本周期2ω1,2ω2の楕円関数であり,積分,
(ただしΩmn=2mω1+2nω2で,Σ′はすべての(m,n)≠(0,0)に対する和)を導入した。これは基本周期2ω1,2ω2の楕円関数であり,積分,
の逆関数である。また,加法公式,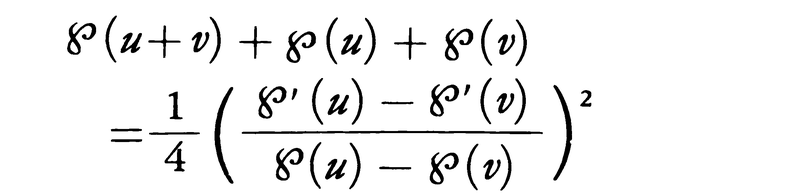
が成り立つ。以上の諸関数と関連して,ワイヤーシュトラスによるζ関数,σ関数,コシグマ関数,ヤコビによる 関数などが導入され,数多くの関係式が知られている。
関数などが導入され,数多くの関係式が知られている。
ヤコビの楕円関数と,ワイヤーシュトラスのそれの関係は,簡単な公式で与えられている。また,任意の楕円関数は,同じ基本周期をもつ と
と ′の有理式で表すことができる。同じ基本周期の二つの楕円関数の間には代数的関係が成り立つ。
′の有理式で表すことができる。同じ基本周期の二つの楕円関数の間には代数的関係が成り立つ。
楕円関数は,数多くの公式によって,広く応用されている。一方,理論的立場からみれば,まず歴史的に複素関数論の一般論の発達を促し,さらに一般化することによって20世紀のリーマン面,代数幾何学の発展を促した。
執筆者:及川 広太郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


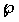 (ペー) 関数,ζ 関数,σ 関数という3つの楕円関数 (ワイエルシュトラスの楕円関数) を定義したが,任意の楕円関数はこのワイエルシュトラスの関数によって表わすことができる。また K.ヤコービは楕円積分の第1種ルジャンドル=ヤコービの標準形の逆関数として sn ,cn ,dn の3つの楕円関数を定義した。
(ペー) 関数,ζ 関数,σ 関数という3つの楕円関数 (ワイエルシュトラスの楕円関数) を定義したが,任意の楕円関数はこのワイエルシュトラスの関数によって表わすことができる。また K.ヤコービは楕円積分の第1種ルジャンドル=ヤコービの標準形の逆関数として sn ,cn ,dn の3つの楕円関数を定義した。