三角関数（読み）サンカクカンスウ（その他表記）trigonometric function

デジタル大辞泉

さんかく‐かんすう〔‐クワンスウ〕【三角関数】

座標の原点Oを中心とする単位円（半径r＝1）と、角θシータが定める動径との交点をP（x,y）とするとき、角θについて、xとyとで表される関数の総称。サイン（正弦関数）・コサイン（余弦関数）・タンジェント（正接関数）・コタンジェント（余接関数）・セカント（正割関数）・コセカント（余割関数）の六つをさす。直角三角形における三角比を一般角に拡張したもの。円関数。

出典　小学館

精選版 日本国語大辞典

さんかく‐かんすう‥クヮンスウ【三角関数・三角函カン数】

1. 〘 名詞 〙 三角比を一般角にまで拡張して得られる関数の総称。正弦関数（サイン）・余弦関数（コサイン）・正接関数（タンジェント）・余接関数（コタンジェント）・正割関数（セカント）・余割関数（コセカント）の六つをいう。円関数。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

三角関数
さんかくかんすう
trigonometric function

直角三角形の辺の比を表す三角比を拡張したもので、任意の角に対して定義される関数である。

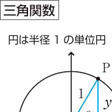
　角は1点Oから出る二つの半直線によって定められる図形であるが、その大きさを決めるため次のように考える。二つの半直線のうち一方を固定して始線とよび、他方は、始線の位置にあった半直線がOを中心として回転して現在の位置まできたものとみる。この半直線を動径という。回転は左回りを正と考え、原点を1回りすれば360度と数える。このようにして、動径の現在位置には、360度の整数倍だけ異なるいろいろな大きさの角が対応することになる。また任意の実数値に対して、それに対応する動径の位置が定まる（図A）。一つの円において、中心角の大きさとそれに対応する弧の長さは比例する。円の半径に等しい長さの弧に対する中心角を1ラジアンとよび、これを単位として角を測る方法が弧度法である。半径rの円周の長さは2πrだから、360度は2πラジアンに相当する。日常生活では度、分、秒を用いる方法が一般的であるが、数学ではもっぱら弧度法が用いられる。そして通常は単位名のラジアンを省略することが多い。ラジアンの呼称は19世紀後期、ジェームズ・トムソンJames Thomsonによって初めて用いられた。

　直交座標を定めた平面上において、x軸の正の部分を始線にとり、角の大きさθに対する動径上に1点Pをとる。OP＝r(r＞0)とし、点Pの座標を(x,y)とすれば、以下の六つの比、x/r, y/r, y/x, x/y, r/x, r/yは、動径上のPの位置には無関係で、θだけによって定まる。これらをθの三角関数といい、次のようによぶ（図B）。

　　x/r＝cosθ
　　（コサインθ、余弦）
　　y/r＝sinθ
　　（サインθ、正弦）
　　y/x＝tanθ
　　（タンジェントθ、正接）
　　x/y＝cotθ
　　（コタンジェントθ、余接）
　　r/x＝secθ
　　（セカントθ、正割）
　　r/y＝cosecθ
　　（コセカントθ、余割）
　原点Oを中心とする半径1の円を単位円というが、cosθ, sinθは角の大きさθに対する動径と円周との交点のx座標、y座標である。このことから、これらの関数は円関数ともよばれる。これら各関数のグラフは図Cに示したとおりである。sinθのグラフの曲線は正弦曲線、あるいはサイン・カーブの名で知られる。

［竹之内脩］

三角関数の性質

以後、点PはOP＝r＝1となるようにとる。すると点Pは動径の現在ある位置のみによって定まり、それが原点の周りを何回転したかには無関係である。このことから、sinθ, cosθはθに2πの整数倍を加えても、その値が変わらないことが知られる。すなわち、これらの関数は、360度あるいは2πを周期とする周期関数である。そのほかの諸関係を表1に示す。次に、cosθ, sinθが単位円周上の点Pのx座標、y座標であることから、ピタゴラスの定理（三平方の定理）によってcos²θ＋sin²θ＝1が得られる。このほかの諸関係を表2に示す。なおcos²θは(cosθ)²の意味である。

　sin(θ＋)をsinθ, cosθ, sin,cosによって表す式などを加法定理という。そして、これらから種々の公式が導かれる。それらを表3に示す。これらの公式を用いると、次のド・モアブルの定理が導かれる。

　　(cosθ＋isinθ)ⁿ＝cosnθ＋isinnθ
ここで、nは整数、iは虚数単位を表す。三角関数の導関数を求めるにあたっては、極限関係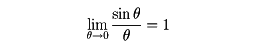

が基本的である。それぞれの関数の導関数、不定積分は表4のようになる。

　x＝Asinct, Acosctは、微分方程式
　　d²x/dt²＝－c²x
を満足する。この微分方程式は、x軸を動く質点が、原点から、その距離に比例する引力を受けるときの質点の運動方程式であり、その運動は、原点を中心とする振幅2A、周期c/2πの往復運動となる。これは、運動のなかの基本的なものと考えられ、これを単振動という。振動現象は、調和解析によって振幅、周期を異にする単振動の重ね合わせとみられる。

　ラジアンで表されたθについての各関数の展開式を表5に示す。

　ド・モアブルの定理からも示唆されるように
　　e^iθ＝cosθ＋isinθ
によって、数eの複素累乗を定義すると、これは、累乗関数の性質e^iθ・eⁱ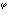＝e^i(θ+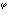)をもつことがわかる（eは自然対数の底(てい)）。この式をオイラーの公式という。そして、一般の複素数z＝α＋iβについて、
　　e^z＝e^α・e^iβ
　　　＝e^α(cosβ＋isinβ)
と定めると、e^zはすべてのzについて表6に示したような展開をもつ関数となり、eの累乗関数の複素数指数への自然な拡張となる。

［竹之内脩］

三角関数の歴史

6種の三角関数を対等に扱うことは、16世紀ビエタに始まるとされる。三角関数の積和公式は10世紀ころからすこしずつ知られるようになった。これは、航海術、天文学における球面三角形の解法に際して、やっかいな積の計算を和で置き換えるために重要なものであった。しかし、17世紀初めの対数の発見により、積を直接計算することが容易にできるようになって、その意味は失われた。三角関数の値を計算するのは、加法定理と図形に頼っていたが、ニュートンが展開式を示し、18世紀初めシャープAbraham Sharp（1651―1742）がこれを用いて製表して以来、展開式が用いられるようになった。現在では、必要な桁(けた)数まで正確に計算するための多項式による計算法その他が案出され、これらは集積回路（IC）に組み込まれて、容易にその値が算出される。

［竹之内脩］

[参照項目] | 加法定理 | 関数 | 弧度法 | 三平方の定理 | 周期関数 | 調和解析 | ド・モアブルの定理 | ニュートン

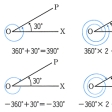
角の大きさの決定〔図A〕

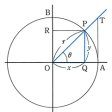
角の大きさθの三角関数〔図B〕

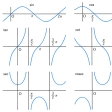
各関数のグラフ〔図C〕

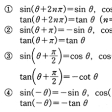
三角関数の性質(1)〔表1〕

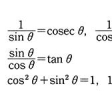
三角関数の性質(2)〔表2〕

三角関数の公式〔表3〕

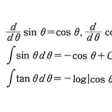
三角関数の導関数と不定積分〔表4〕

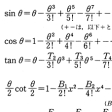
三角関数の展開式〔表5〕

eの複素累乗〔表6〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

三角関数 (さんかくかんすう)
trigonometric function

三角関数は，最初は直角三角形の一つの鋭角によって定まる辺の長さの比，いわゆる三角比として定義せられ，それが一般の角に拡張された。それらに関して後述の加法定理などの性質や，別の項目で述べられる三角形の正弦定理，余弦定理が導かれ，古くから測量問題などに応用された。現代では，三角形という図形的意味とは独立に，数学の研究対象としての地位を確立し，解析学において重要な関数となっている。

三角比

∠C＝90°の直角三角形ABCにおいて，次の6個の比の値は，角Aの大きさのみで定まり，直角三角形ABCの大きさには無関係である（図1）。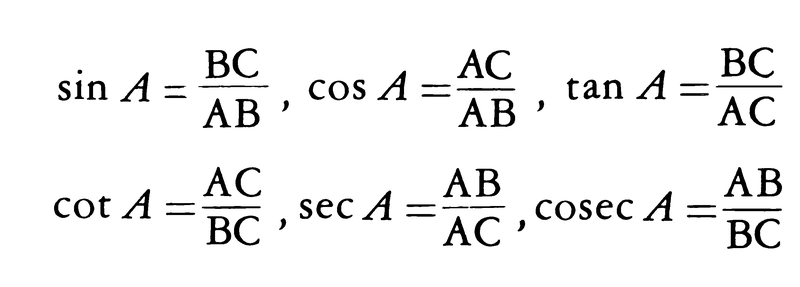

これらの比の値を，それぞれ角Aの正弦（サインsine，記号sin），余弦（コサインcosine，記号cos），正接（タンジェントtangent，記号tan），余接（コタンジェントcotangent，記号cot），正割（セカントsecant，記号sec），余割（コセカントcosecant，記号cosec）といい，これらを総称して三角比という。次に述べる三角関数は三角比の概念の拡張であって，角θが鋭角（0°＜θ＜90°）の場合は上の三角比の定義と一致する。

三角関数

平面上で定点のまわりの回転を考えるときは360°以上の角も考える。また，回転の向きを区別するために，角に正負の符号をつける。すなわち，時計の針の回る向きと反対向きの回転角を正の角，時計の針の回る向きと同じ向きの回転角を負の角と定める（図2）。

　rを正の定数とし，座標平面上で，原点Oのまわりに長さrの線分OPが回転し，x軸の正の方向から角θだけ回転したときの点Pの座標を（x，y）とすると，次の6個の比の値はθのみで定まり，線分OPの長さrには無関係である（図3）。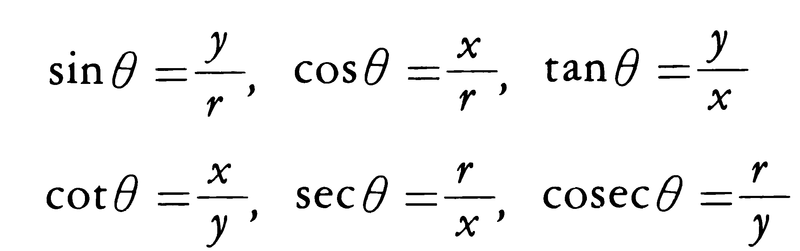

これらの値をθの関数と考え，前に述べた三角比の名称に対応して，それぞれ正弦関数，余弦関数，正接関数，……といい，これらを総称して三角関数という。sinθとcosθはすべての実数θに対して定義されるが，他の関数については，上の式の分母が0になるような点Pに対応するθは定義域から除いて考える。

　nが2以上の整数のとき，かつその場合に限り，例えば（sinθ）ⁿをsinⁿθとも書かれる。他の三角関数についても，それは同様である。

　三角関数の間には次の関係がある。

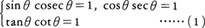
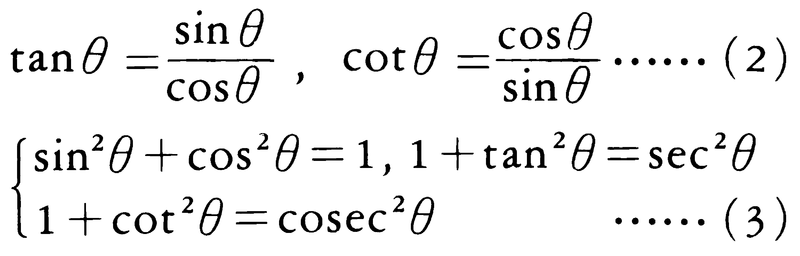
　今後，三角関数の変数θは弧度法による数値とする。

　tanθとcotθはπを周期とする周期関数であり，その他の三角関数は2πを周期とする周期関数である。またsinθ，tanθ，cotθ， cosecθは奇関数であり， cosθ， secθは偶関数である。

　さらに次の式が成立する。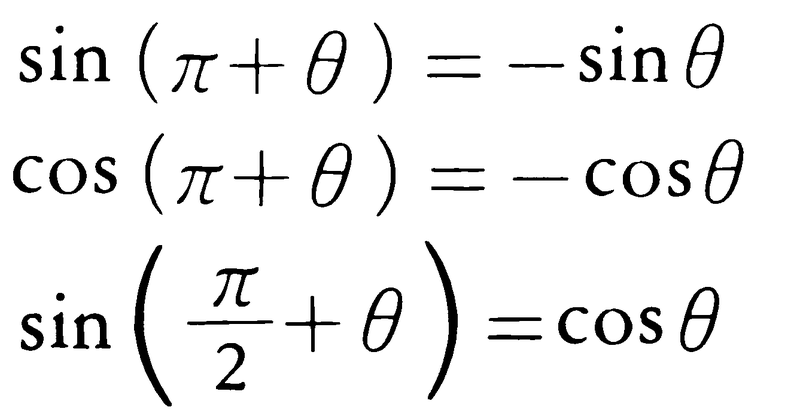



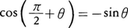
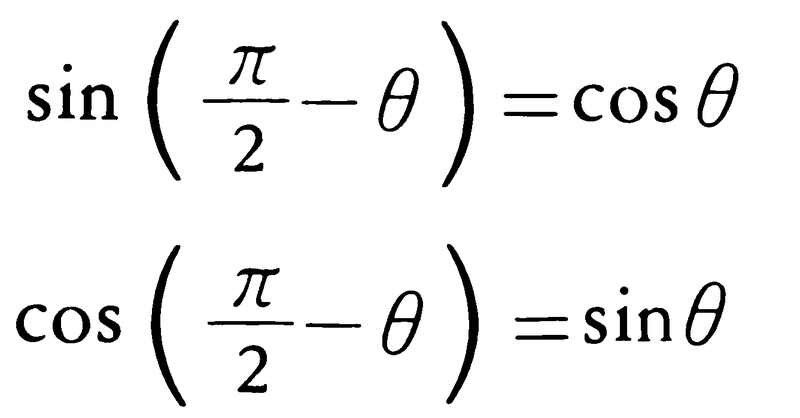
これらの式と（1）（2）とを組み合わせて，tanθ，cotθなどに関する同様な式が容易に導かれる。

三角関数の加法定理

任意のα，βに対して次の式が成り立つ（複号同順）。これらを三角関数の加法定理という。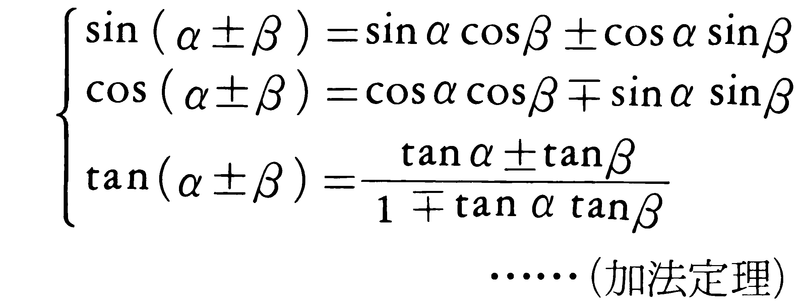

この加法定理から，次の2倍角の公式，3倍角の公式，半角の公式，

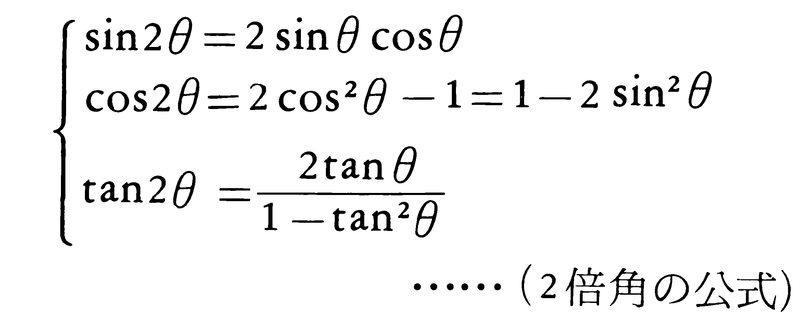
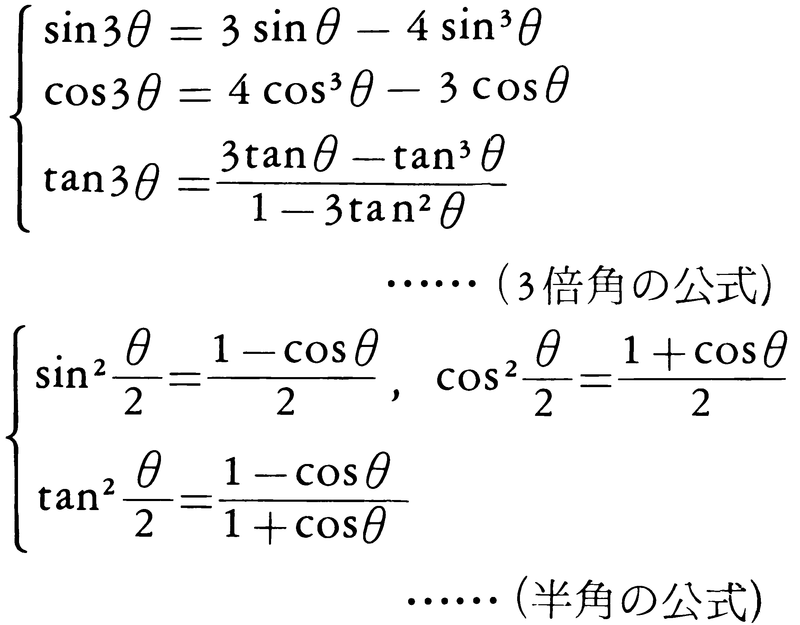
正弦・余弦の積を和に変える公式，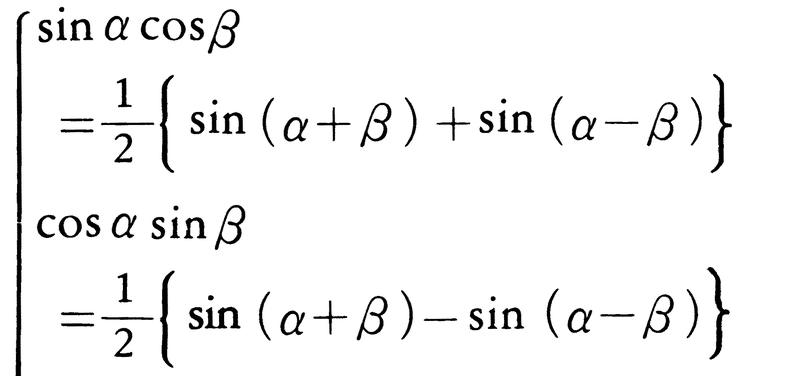

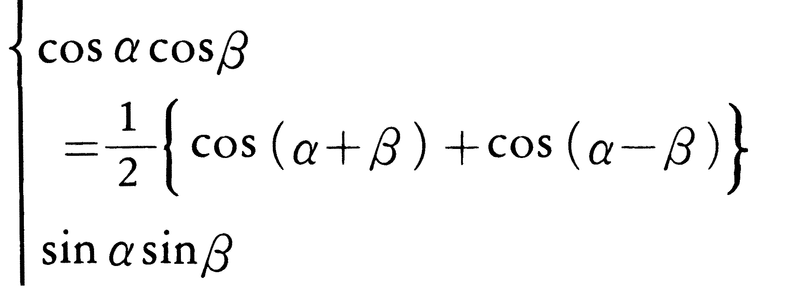
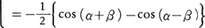
和を積に変える公式，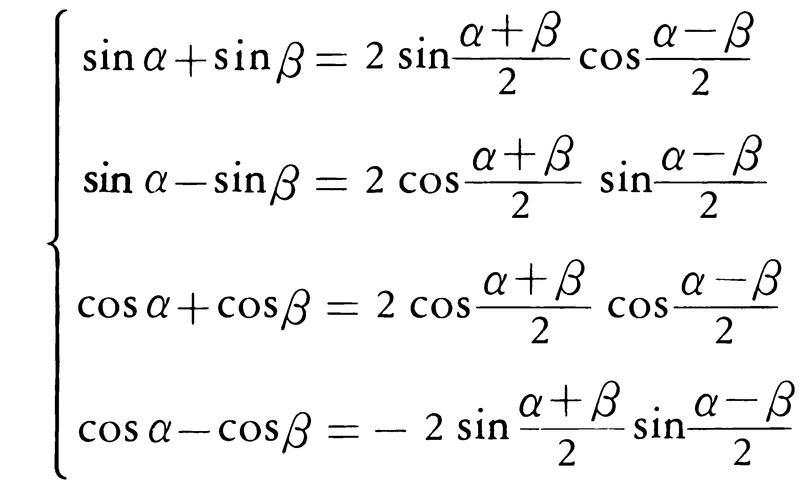

が導かれる。

　次の公式はド・モアブルの定理と呼ばれ，複素数の累乗，累乗根などの計算に使う。nを正の整数，iを虚数単位とすると，

　（cosθ＋isinθ）ⁿ＝cosnθ＋isinnθ

単振動

図3において，OPが一定の角速度ωで回転しているとし，時間t＝0のときθ＝αであったとする。Pからx軸，y軸に垂線PQ，PRをおろすと，点Q，Rはそれぞれx軸，y軸上で時間tの関数として，

　x＝rcos（ωt＋α），y＝rsin（ωt＋α）

で表される運動をする。上のyの式は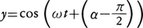，とも書けるから，xの式と本質的に同じと考えてよい。このような運動を単振動という。振子の往復運動は，振幅が小さいときはこの式で表される。

三角関数の微分，積分

今後，三角関数の変数は，角の概念を離れて一つの実数と考え，文字xで表すことにする。関数sin xの導関数を（sin x）′と書くことにすると，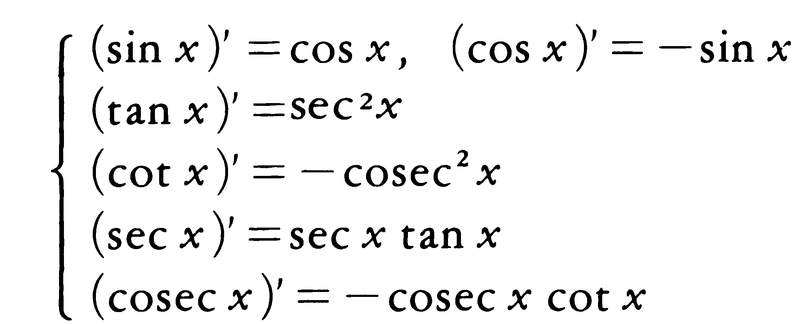

が成立する。とくにcosxとsinxはすべてのxにおいて何回でも微分可能で，さらに，次のようにべき級数に展開される。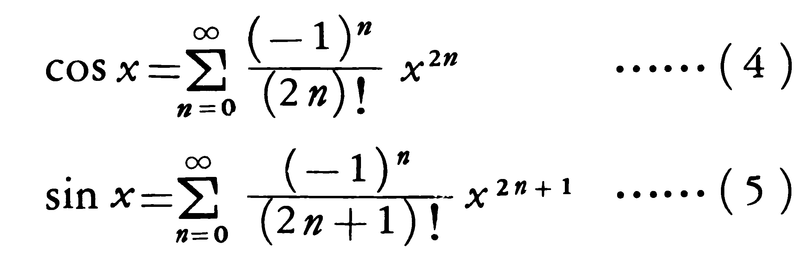

上の微分法の公式から，その逆演算としての不定積分の公式が得られるが，とくに定積分に関して次の〈直交性〉が成り立ち，フーリエ級数論の基礎となる。m，nを整数として，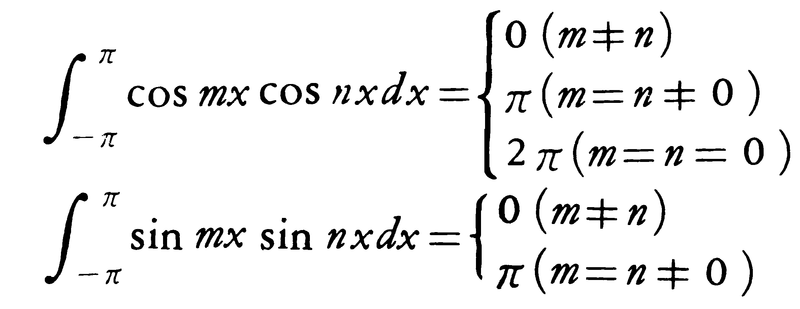

複素変数の三角関数

（4）（5）において実数の変数xを複素数zで置き換えると，右辺のべき級数は任意の複素数zに対して収束する。これらのべき級数で複素変数zの関数cosz，sinzを定義すると，それらは初めの実数xの関数cosx，sinxの拡張であり，前に述べた加法定理などの公式は，すべて複素変数の関数cosz，sinzに対しても成立する。

　また，複素変数の指数関数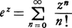，を用いると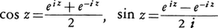，と表され，e^iz＝cosz＋isinzが成立する。とくにz＝iθ（θは実数）とした式，

　e^iθ＝cosθ＋isinθ

をオイラーの公式Euler's formulaという。
執筆者：伊藤 清三

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

三角関数【さんかくかんすう】

円関数とも。直角三角形の３辺間に成立する比（三角比）を一つの角の関数と考えたもの。サインsin，コサインcos，タンジェントtan，コタンジェントcot，セカントsec，コセカントcosecの六つ。角度を度分秒で表した数値が三角関数表にまとめられている。理論上は角度をラジアンで表し，あらゆる大きさの角度について一般的に定義される。すなわち平面上に直交軸O-xyをとり，偏角Φ，長さrの動径の先端の座標を（x，y）とすれば，sin Φ＝y/r，cos Φ＝x/r，tan Φ＝y/x，cot Φ＝x/y，sec Φ＝r/x，cosec Φ＝r/y。tan Φ，cot Φは周期π，他は周期２πの１価周期超越関数（変数と定数によって代数的に表すことのできない関数。代数関数を参照）。→逆三角関数／三角法／三角測量
→関連項目コサイン｜コセカント｜コタンジェント｜サイン｜サインバー｜三角形｜正弦波｜セカント｜双曲線関数｜タンジェント

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

三角関数
さんかくかんすう
trigonometric function

円関数ともいう。直交座標系 O－xy において，Ox を始線，また O を中心として回転する定線分 OP＝r を考えて，これを動径と呼ぶ。いま動径 OP が始線から左回りに回転して得られる角の大きさを θ ，P の座標を (x，y) とすれば，θ の関数 sin ， cos ， tan ，cosec ， sec ， cot は，次のように定義される。
ただし r＞0 ，正接，正割では x≠0 ，余割，余接では y≠0 とする。これらの関数を総称して三角関数という。三角関数は周期関数であって，θ をラジアンで測ったとき，正接，余接は π ，他は 2π を基本周期とする。 θ があらゆる実数値をとるときの三角関数のとりうる値の範囲は，それぞれ ｜ sin θ｜≦1 ，｜ cos θ｜≦1 ，｜ tan θ｜＜∞ ，｜ cot θ｜＜∞ ，1≦｜ sec θ｜＜∞ ，1≦｜cosecθ｜＜∞ 。また，三角関数相互間には tan θ＝ sin θ/ cos θ ， cot θ＝ cos θ/ sin θ ， sin ²θ＋ cos ²θ＝1 などの関係がある。国によっては， tan を tg ， cot を ctg ，cosec を csc と書く流儀もある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の三角関数の言及

【平面三角法】より

…Pの座標が(a,b)で線分OPの長さがrならば，6個の比b/r,a/r,b/a,a/b,r/a,r/bはPのとり方によらずαによって定まる。それで，これらをそれぞれsinα,cosα,tanα,cotα,secα,cosecαで表して，∠αのサイン(正弦)，コサイン(余弦)，タンジェント(正接)，コタンジェント(余接)，セカント(正割)，コセカント(余割)と呼び，総称して三角比，またはαの関数と考えて三角関数と呼ぶ。平面三角法とは三角関数に関する諸公式，三角関数を用いて書き表される三角形の辺と角に関する諸公式およびそれらの測量などへの応用を学ぶ学科である。…

※「三角関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」