改訂新版 世界大百科事典 「剰余系」の意味・わかりやすい解説
剰余系 (じょうよけい)
complete residue system
自然数mに対して，二つの整数aとbのmで割った余りが等しいとき，aとbはmを法として合同であるという。この関係で整数全体をクラス分けすると，m個の類（クラス）に分かれる。これらの類を剰余類といい，この各類から一つずつ元を取り出した組を剰余系という。例えばm＝6とすれば，0，1，2，3，4，5は1組の剰余系である。また，6，－5，8，9，－2，－1も剰余系である。mと互いに素な整数からなる類を既約剰余類といい，その各類から一つずつ元を選び出して得られた整数の組を既約剰余系という。m＝6のとき，1，5は既約剰余系である。mを法とする既約剰余類の個数φ（m）によって定められる関数φをオイラー関数という。mとnが互いに素な自然数であるとき，φはφ（mn）＝φ（m）φ（n）という関係を満たし，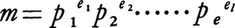
をmの素因数分解とすると，φ（m）は，
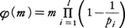で与えられる。
執筆者：斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報