場合の数（読み）バアイノカズ

デジタル大辞泉

ばあい‐の‐かず〔ばあひ‐〕【場合の数】

さいころの目の出方など、ある事柄の起こりうる場合の総数。

出典　小学館

精選版 日本国語大辞典

ばあい【場合】 の 数(かず)

1. 数学で、ある情況の下に起こりうる場合の総数。たとえば、さいころを振ったときの目の出方の総数（すなわち６）、四個のものを任意に並べたときにできる列の総数（すなわち２４）など。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

場合の数
ばあいのかず

いくつかの事柄について「全部で何通りの場合があるか」数え上げるような問題を「場合の数」を求める問題とよんでいる。この種の問題において基礎となるのは次の二つの法則である。

［植竹恒男］

和の法則

二つの事柄A、Bがあって、おのおののおこり方がそれぞれm、n通りで、それらがともにおこることがなければ、AかBがおこる場合の数はm+n通りだけある。このとき、l通りが重複しておこったとすれば、AかBがおこる場合はm+n-lとなる。

［植竹恒男］

積の法則

二つの事柄A、Bがあって、Aのおこり方m通りのおのおのに対してBのおこり方がn通りずつあれば、AとBがこの順序でおこる場合の数はm×n通りになる。

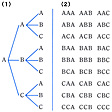
　これらの法則は、三つ以上の事柄についても同様に成り立つ。たとえば、三つの文字を並べてつくられる文字列の個数は、同じ文字を何回でも使ってよいとすれば、最初の文字の選び方は三通りあり、そのおのおのに対して第二の文字の選び方も三通りある。そのおのおのに対して最後の文字の選び方も三通りあるから、全部で3×3×3=27通りになる。このうち、たとえばAで始まる文字列を具体的につくるのに図(1)のような図が用いられる。B、Cから始まる文字列についても同様な図を描くことができる。このような図を樹形図(じゅけいず)という。これらの文字列を辞書式の順序に書き並べたものが図(2)である。

［植竹恒男］

[参照項目] | 順列・組合せ

場合の数（樹形図の例）〔図〕

出典　小学館　日本大百科全書(ニッポニカ)