順列組合せ（読み）ジュンレツクミアワセ

デジタル大辞泉

じゅんれつ‐くみあわせ〔‐くみあはせ〕【順列組（み）合（わ）せ】

数学で、順列と組み合わせ。

出典　小学館

日本大百科全書(ニッポニカ)

順列・組合せ
じゅんれつくみあわせ

n個の異なるものからr個を取り出して1列に並べたものをn個からr個とる順列といい、その総数を_nP_rと書く（Pは、順列の英語permutationの頭文字をとったもの）。たとえば、4個の文字A、B、C、Dから3個をとって並べると、次のような24通りの順列ができる。したがって、₄P₃＝24である。

　　ABC ABD ACB ACD ADB ADC
　　BAC BAD BCA BCD BDA BDC
　　CAB CAD CBA CBD CDA CDB
　　DAB DAC DBA DBC DCA DCB
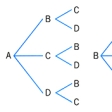
　順列は、図Aのような樹形図を書くと考えやすい。一般に「二つの事柄A、Bがあって、Aのおこり方がm通りあり、そのおのおのに対して、Bのおこり方がn通りずつあれば、AとBが引き続いておこる場合の数はm×nである」が成り立つ。これを積の法則というが、このことから図Aによって容易にわかるように₄P₃＝4×3×2が得られ、一般に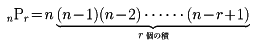

となる。この式の右辺は、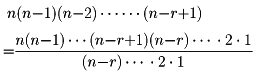

と変形できるから、階乗！を用いると、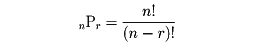

と表される。とくにn個からn個とる順列、すなわち、n個の異なるものを1列に並べてできる順列の総数は_nP_n＝n！である。

　n個の異なるものからr個を取り出してできる各組を、n個からr個とる組合せといい、その総数を_nC_rまたは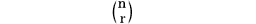

と書く（Cは、組合せの英語combinationの頭文字をとったもの）。これは順列において順序を考えに入れない場合である。たとえば、4個の文字A、B、C、Dから3個をとってできる組合せは
　　｛A, B, C｝,｛A, C, D｝,｛A, B, D｝,｛B, C, D｝
の4通りである。したがって₄C₃＝4である。この値は次のように₄P₃からも求められる。₄P₃個の順列のなかには、組合せとして同じものが₃P₃＝3！＝6個ずつ含まれている。したがって₄P₃＝3！₄C₃ゆえに
　　₄C₃＝₄P₃/3！＝24/6＝4
一般に、_nP_r＝n！_nC_rが成り立ち、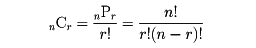

この式でr＝0とすれば、形式的に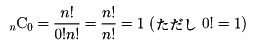

が得られる。_nC_rはn個の要素からできている集合の部分集合でr個の要素をもつものの総数に等しい。_nC₀はそれらの部分集合のなかの「要素をもたないもの」すなわち空集合を1個と数えたことに相当する。

［植竹恒男］

組合せに関する公式

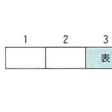
1枚の硬貨を6回投げるとき、表が2回だけ出る場合は何通りあるか考えてみよう。1、2、……、6回目に出た結果を図Bのように書き入れていくと、これらの六つの枠のうちから二つを選んで「表」と記入し、残りは「裏」とすれば、条件に適する組合せが一つできる。よって、求める場合の数は₆C₂＝(6・5)/2！＝15となる。この問題は、六つの枠から四つを選んで「裏」と記入し、残りを「表」と考えて、₆C₄＝(6・5・4・3)/4！＝15としても解ける。同様に考えて、一般に
　　_nC_r＝_nC_n-r
が成り立つ。また、次の等式も成り立つ。

　　_n-1C_r＋_n-1C_r-1＝_nC_r
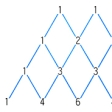
　図Cのように、この関係を利用して_nC_rの値を順次求めていくのがパスカルの三角形である。

［植竹恒男］

いろいろな順列

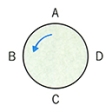
A、B、C、Dの4人が丸テーブルに着席する仕方は全部で何通りあるだろうか。この場合は図Dのように、4人が一つずつ順送りに位置を変えてできる四つの並び方はすべて同じものとみられる。図Dのように、一番上から始めて時計と逆回りにとった四つの順列をABCD, DABC, CDAB, BCDAで表す。4人が1列に並ぶ順列の数4！＝24のなかには、このような意味で「同じ」順列が四つずつあるから、求める場合の数は4！/4＝3！＝6となる。一般に、n人が丸テーブルに着席する仕方は全部でn！/n＝(n-1)！通りある。また、n人からr人を選んでこのように並ぶ仕方は全部で_nP_r/r通りある。このような順列を円順列という。n個の玉で数珠(じゅず)やネックレスをつくる場合は、さらに図Dを裏返しにしたものも「同じ」とみなされるから、円順列の数の半分になる。このような順列を数珠順列とよぶ。

　4個の文字A、B、C、Dから3個の文字を取り出して並べる場合、同じ文字を何回使ってもよいとすれば、どの文字についても4通りの選び方があるから、全部で4×4×4＝4³＝64通りあることになる。一般に、n個の異なるものから同じものを重複してとることを許してr個とる順列を重複順列(ちょうふくじゅんれつ)といい、その総数はn^rとなる。

［植竹恒男］

『C・L・リウ著、伊理正夫他訳『組合せ数学入門Ⅰ』（1972・共立全書）』

[参照項目] | 階乗 | 二項定理

順列の例（樹形図）〔図A〕

組合せの例〔図B〕

パスカルの三角形〔図C〕

いろいろな順列〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

順列・組合せ (じゅんれつくみあわせ)
permutations and combinations

n個の互いに区別のつくものからr個取って，ある順序に並べたものを順列という。そのような並べ方，すなわちn個のものからr個を取った順列が全部でいくとおりあるかは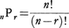，＝n（n－1）……（n－r＋1）で与えられる。また，異なるn個のものからr個を取り出し順序は考えないとき，それを組合せという。n個からr個を取る組合せの数は_nC_rまたは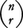で表され，

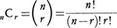である。例えば，10人の人から4人を選んで一列に並べる順列の数は，₁₀P₄＝10・9・8・7＝5040であり，6チームで，各2チームが1回ずつ対戦するリーグ戦を行うとき，試合数は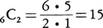である。

　_nC_rについて次のような等式が成り立つ。

　（1）_nC_r＝_nC_n-r

　（2）_nC_r＝_n-1C_r-1＋_n-1C_r

（1）は，n個のものの中からr個を取り出す各組合せと，n個のものの中からそのr個を取りのぞいた残りのn－r個の組合せとが1対1に対応することに相当する。（2）は，n個のものからr個を取る組合せの数は，そのうち特定の1個を含む組合せの数_n-1C_r-1と，特定の1個を含まない組合せの数_n-1C_rの和に等しいということに相当する。

重複順列・重複組合せ

n個の相異なるものから重複を許してr個取り出して並べる順列を重複順列という。この重複順列の数は，n^rである。また，n個の相異なるものから重複を許して，r個取る組合せを重複組合せという。その数は_nH_rで表され，_nH_r＝_n+r-1C_rである。_nH_rはn変数の単項式のうち次数がrであるものの数と一致する。例えば3変数x，y，zの三次の単項式は全部で，x³，y³，z³，x²y，x²z，xy²，y²z，xz²，yz²，xyzの10個であるが，これは₃H₃＝₅C₃＝10と計算することができる。また，rが一つの自然数であるとき，z₁＋z₂＋……＋z_n＝rの負でない整数の解（z₁，z₂，……，z_n）の数は_nH_rである。

同じ物があるときの順列

p個のミカン，q個のリンゴ，r個のメロン，全部合わせてn＝p＋q＋r個の果物を一列に並べるしかたは，n！/（p！q！r！）とおりである。この順列の数は，（x＋y＋z）ⁿを展開したときのx^py^qz^rの係数に等しい。もっと多くの種類のあるときも同様である。

円順列

4個のものを四つの場所におく方法は，4！＝24とおりであるが，いま，この四つのものを円周に沿って並べる場合，例えば次のような四つの順列は，

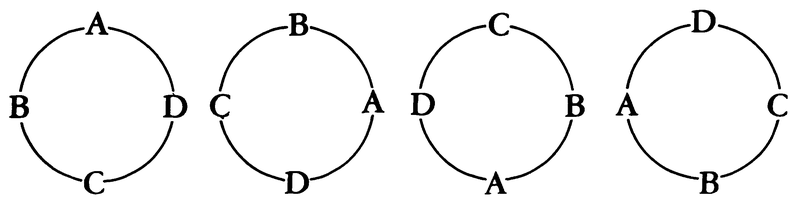
A，B，C，Dの順序関係は同一であるので同一のものと考えることにすれば，4個のうちのどれか一つ，例えばAの場所を決めておき，残りの三つの並べ方を考えればよいから，この順列の数は（4－1）！＝6である。このような順列を円順列という。n個のものからr個取って円周上に並べる円順列の数は，

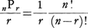
じゅず順列

n個の異なった玉からr個を取ってじゅずを作るとき，玉の並べ方の数は，円順列の半分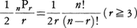，で与えられる。じゅずを裏返したとき，同一円順列となるものは同じじゅずだと考えられるからである。ただし，r＝1，2のときは特別で，それぞれ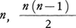となる。
執筆者：杉江 徹

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の順列組合せの言及

【確率】より

…また同じころ，イギリスのJ.グラウントによる生命表の作成などの統計的研究も確率論の発生を促したとされる。次いで18世紀に入り，ヤコブ･ベルヌーイの遺稿が，甥のニコラウスによってまとめられ，《推測法》(1713)として出版されたが，そこには順列，組合せを用いた確率の話が出てきて，しだいに確率論としての形態を整えてきたのであった。　ここでも創生期のように有限個の事象を扱った確率から話を始める。…

※「順列組合せ」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」