射影変換
しゃえいへんかん
projective transformation
配景対応を有限回続けて行うことにより,1つの図形を他の図形の上へ対応させる (変換する) ことをいう。配景対応を1つの関数と考えれば,この射影変換は,合成関数 (積関数) に相当する。たとえば図において,O1 を中心として平面 π を平面 π' に移す配景対応 f1 ,O2 を中心として π' を π に移す配景対応を f2 とすれば,f1 ,f2 を続けて行うことによって得られる対応 f は射影変換である。この図において,
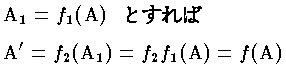 すなわち,π 上の点Aは f1 によって π' 上の点 A1 に移され,続いてこの A1 が f2 によって π 上の点 A' に移される。それゆえ f は,π 上の点 A を,同じ π 上の点 A' に移す変換である。座標では,斉次座標での1次変換で表現される。
すなわち,π 上の点Aは f1 によって π' 上の点 A1 に移され,続いてこの A1 が f2 によって π 上の点 A' に移される。それゆえ f は,π 上の点 A を,同じ π 上の点 A' に移す変換である。座標では,斉次座標での1次変換で表現される。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の射影変換の言及
【幾何学】より
…これによれば,例えば,ユークリッド幾何学はユークリッド空間と合同変換(ユークリッド空間のそれ自身の上への1対1対応で任意の2点間の距離を変えないもの)のつくる群で定まり,合同変換で不変な長さや面積などを研究する幾何学となる。また,射影幾何学は射影空間(無限遠点も含めた空間)と射影変換(射影空間のそれ自身の上への1対1対応で直線を直線にうつすもの)のつくる群で定まり,射影変換で不変な結合性質や非調和化などを研究する幾何学となる。さらに,双曲幾何学は射影空間内のある二次曲面Qの内部のみを空間とみて,Qを不変にするような射影変換のつくる群を考えれば,これに対応する幾何学として規定でき,Qとしてある虚の二次曲面を考えることにより楕円幾何学も同様に規定できる。…
【射影幾何学】より
…いろいろな点からの配景対応を次々と有限回続けて行うことにより,最初の射影平面から最後の射影平面の上への1対1対応が得られるが,これを射影対応という。とくに一つの射影平面からそれ自身の上への射影対応を射影変換という。一つの射影平面上の射影変換の全体は群をつくる。…
※「射影変換」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
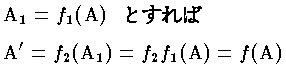 すなわち,π 上の点Aは f1 によって π' 上の点 A1 に移され,続いてこの A1 が f2 によって π 上の点 A' に移される。それゆえ f は,π 上の点 A を,同じ π 上の点 A' に移す変換である。座標では,斉次座標での1次変換で表現される。
すなわち,π 上の点Aは f1 によって π' 上の点 A1 に移され,続いてこの A1 が f2 によって π 上の点 A' に移される。それゆえ f は,π 上の点 A を,同じ π 上の点 A' に移す変換である。座標では,斉次座標での1次変換で表現される。

