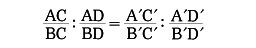配景対応（読み）はいけいたいおう

日本大百科全書(ニッポニカ)

配景対応
はいけいたいおう

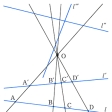
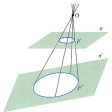
一つの図形が、他方の図形の射影の切断になっているとき、これらの図形の間の対応をいう。ここで射影とは、図形Fの各点とF外の1点Oとを結ぶ直線を引くことをいう。図Aでは、平面上で直線l上の図形F（4点A、B、C、Dのこと）を、図Bでは、空間で平面π上にある図形Fを、それぞれOから射影している。このようなOを通る直線の集合（直線束）に対して、図Aのl′、l″、l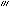や、図Bのπ′のように、Oを通らない直線や平面を描いて交点を求めるのが切断または截断(せつだん)である。二つの図形は、その間に配景対応をつけるような点Oをちょうどみつけることができれば、Oを中心とする配景の位置にあるという。配景対応によって線分の長さの比は、図AのAB:BC≠A′B′:B′C′のように、一般に変わるが、非調和比は変わらない。つまり、

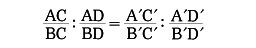
である。

［立花俊一］

[参照項目] | 射影対応

配景対応説明図〔図A〕

配景対応説明図〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

配景対応
はいけいたいおう
perspective correspondence

1つの直線 l 上に並んでいる点 A，B，C，…，P，… の集合を点列と呼んで，l(A，B，C，…，P，…) で表わす。また1つの点 L を通って同一平面にある直線 a，b，c，…，p，… の集合を線束と呼んで，L(a，b，c，…，p，…) で表わす。1つの点列 l(A，B，C，…，P，…) の要素と，1つの線束 L(a，b，c，…，p，…) の要素間に一対一の対応が存在して，点Pに対応する直線 p は点 P を通り，直線 p に対応する点 P は直線 p の上にあるならば，この対応を配景対応と呼ぶ。なお，図の点列 l(A，B，C，…，P，…) と点列 l'(A'，B'，C'，…，P'，…) ，線束 L(a，b，c，…，p，…) と線束 L'(a'，b'，c'，…，p'，…) も互いに配景対応にあるといわれる。配景変換ともいう。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の配景対応の言及

【射影幾何学】より

…このようにすれば，点Oからの中心射影で，m上の点は上の無限遠点にうつり，上の無限遠点はn上の点にうつって，上の点と上の点が1対1に対応し，また上の直線と上の直線が1対1に対応する。，のように平面にその上の無限遠点をつけ加えたものを射影平面といい，上で述べたからの上への1対1対応を点Oからの配景対応という。平面α,βとこれらに平行でない直線lが与えられたとき，α上の点Pに対し，その点を通りlに平行な直線がβと交わる点Qを対応させる対応(平行射影)を考えても，上の点，直線と上の点，直線に関し上と同様のことがいえる。…

【配景】より

…空間に異なる2平面α,α′とこれらの上にない1点Cがあるとき，Cを通る任意の直線がα,α′と交わる点をP,P′として，PとP′とを対応させれば，無限遠点も含めて考えるとき，α上の点とα′上の点とは1対1に対応する。この対応を，Cを中心とする配景対応という(図1)。平面上に異なる2直線a,a′とこれらの上にない1点Cがあるときも，a上の点とa′上の点の間に1対1対応が同様に定義される。…

※「配景対応」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」