一次変換（読み）いちじへんかん（その他表記）linear transformation

精選版 日本国語大辞典

いちじ‐へんかん‥ヘンクヮン【一次変換】

1. 〘 名詞 〙
2. ① ベクトル空間からベクトル空間へのある種の写像。ベクトル空間Ｕからベクトル空間Ｖへの写像ｆのうち、f(αa+βb)=αf(a)+βf(b) （ａ、ｂはＵの要素、α、βは実数）をみたすものをＵからＶへの一次変換という。
3. ② 複素数に複素数を対応させるある種の写像。z′=(az+b)/(cz+d) という形で表わされるようなもの。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

一次変換 (いちじへんかん)
linear transformation

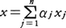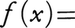
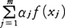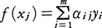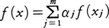
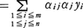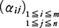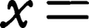
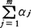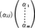直線，平面，空間のように座標が定まっているものの間の写像で，座標について一次式で表されるものを一次変換という。例えば座標X，Y，Zが定まった空間の間の写像fで，点（x，y，z）をf（x，y，z）＝（a₁x＋b₁y＋c₁z，a₂x＋b₂y＋c₂z，a₃x＋b₃y＋c₃z）に移すものは一次変換である。この考えは，一般のn次元線形空間Vからm次元線形空間Wへの写像fに拡張される。x₁，……，x_nをVの基底，y₁，……，y_mをWの基底とする。Vの元xを（α_j：スカラー）と書けば，となり，このときfは一次変換といわれる。各f（x_j）はWの元であるから，（α_ij：スカラー）と書ける。一次変換の性質から，となり，fは（m，n）行列で完全にきまる。Vの元を列ベクトルで表示すれば，変換f（x）は行列の積で表せる。一次変換は無限次元空間でも同じように考えられる。一次変換は線形空間の間の線形写像と実質的に同じであり，一次変換という言葉で線形写像を意味することもある。また，一次分数変換のことを単に一次変換ということもある。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

1次変換
いちじへんかん
linear transformation

線形写像ともいう。 xy 平面上で，点 (x₁，x₂) を点 (y₁，y₂) に移す変換の規則が，1次式 y₁＝a₁₁x₁＋a₁₂x₂，y₂＝a₂₁x₁＋a₂₂x₂ ( a_ij は定数) で与えられるとき，これを (x₁，x₂) から (y₁，y₂) への1次変換という。この1次変換を，ベクトル x＝(x₁，x₂) をベクトル y＝(y₁，y₂) へ移す変換であるとみなし，右辺の係数の配列を，行列 A＝(a_ij) で表わせば，この変換は，
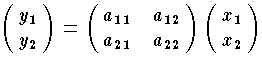すなわち y＝Ax と書ける。一般に，ベクトル空間 V₁ から V₂ への変換 y＝f(x) が，V₁ の任意の元 x，x' ，およびスカラー λ，λ' に対して f(λx＋λ'x')＝λf(x)＋λ'f(x') を満足するとき，f を V₁ から V₂ への線形写像といい，特に V₁ のそれ自身への線形写像を1次変換と呼ぶ。有限次元の場合，V₁，V₂ に基底を定めておけば，f は行列を使って y'＝Ax という形で表わせる。関数論においては，1次分数式
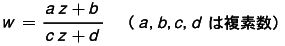で表わされる w から z への変換 w＝Tz を1次変換ということがある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の一次変換の言及

【座標】より

…簡単な例として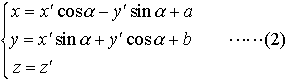，は，原点をxy平面内で点(a,b)に平行移動し，さらにその点のまわりに角度αの回転を行った直交座標系(x′，y′，z′)によってもとの(x,y,z)を表す場合である。一般に旧座標系｛x_i｝が新座標系｛x_i′｝の一次式の場合，すなわち(1)が具体的に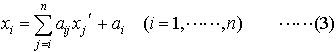，で与えられるような座標変換は一次変換と呼ばれ，行列の記法を用いてx＝Ax′＋aで示すことができる。ここでA＝(a_ij)はa_ijを要素とするn行n列の行列，a＝(a_i)はn次の列ベクトル(n行1列行列)である。…

※「一次変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」