小行列式（読み）しょうぎょうれつしき（その他表記）minor determinant

改訂新版　世界大百科事典

小行列式 (しょうぎょうれつしき)
minor determinant

（m，n）行列A＝（a_ij）を考える。Aのi₁，……，i_r行とj₁，……，j_r列（i₁＜……＜i_r，j₁＜……＜j_r）の交点にある成分からなる行列，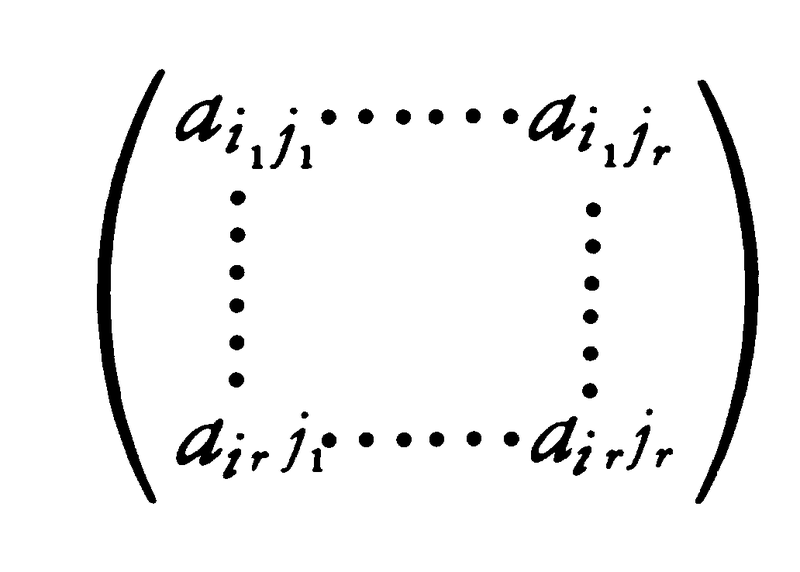

として得られるものを，Aのr次の小行列，またその行列式を，Aのr次の小行列式という。後者を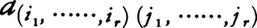と書くことがある。行列Aの階数がrであるための必要十分条件は，r次の小行列式の中に0でないものがあり，（r＋1）次の小行列式の中にはそういうものがないことである。Aがn次の正方行列の場合，｛1，……，n｝から｛i₁，……，i_r｝を除いた自然数の小さい順に並べたものを（i_r+1，……，i_n）と書くことにし，i₁＋……＋i_r＝i，j₁＋……＋j_r＝jとして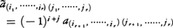，とおく。これは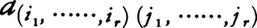の余因子といわれる。（i₁，……，i_r），（j₁，……，j_r）を固定すると，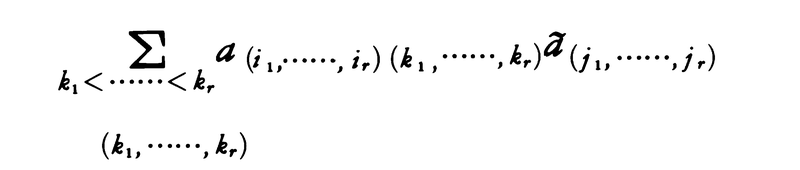



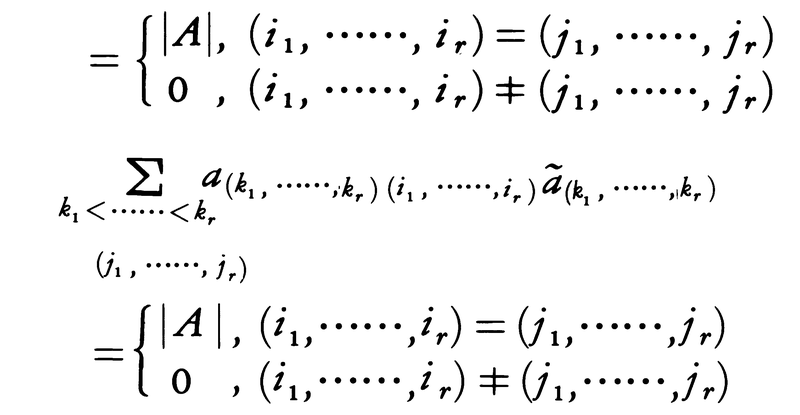
これは行列式のある行または列についての展開の一般化になっており，ラプラスの展開定理といわれる。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

小行列式
しょうぎょうれつしき
minor determinant

n 次の行列式の第 p₁，p₂，…，p_m 行と，第 q₁，q₂，…，q_m 列を取去った残りの，n－m 次の行列式を
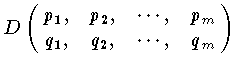と書き，D からつくられる n－m 次の小行列式と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典