相反方程式（読み）そうはんほうていしき

日本大百科全書(ニッポニカ)

相反方程式
そうはんほうていしき

次のように、係数が左右対称な代数方程式を相反方程式という。

　　〔1〕a_nxⁿ+a_n-1x^n-1+
　　　　　……+a₁x+a₀=0
　　　　　(a_n=a₀≠0,
　　　　　 a_n-1=a₁,……)
　相反方程式の解は、より低次の方程式の解に帰着させることができる。

（1）偶数次の場合　nが偶数2mのときには、〔1〕の両辺をx^mで割って、x+(1/x)=tと置くと、tのm次の方程式が得られる。たとえば、
　　x⁴+3x³-2x²+3x+1=0
のときは、x²で割って
　　〔2〕

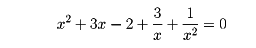
ここでx+(1/x)=tと置くと、〔2〕はt²+3t-4=0となる。

（2）奇数次の場合　〔1〕は次の形になる。

　　(x+1)・g(x)=0
ここでg(x)=0は、偶数次の相反方程式である。たとえば、
　　x⁵-2x⁴+3x³+3x²-2x+1=0
は(x+1)(x⁴-3x³+6x²-3x+1)=0
となる。

［寺田文行］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

相反方程式
そうはんほうていしき
reciprocal equation

n 次の代数方程式を

f(x)＝a₀xⁿ＋a₁x^n-1＋…＋a_n-1x＋a_n＝0

とし，その n 個の根を α₁ ，α₂ ，…，α_n とするとき，そのおのおのの逆数 1/α₁ ，1/α₂ ，…，1/α_n を根にもつ代数方程式は，初めの方程式の x に 1/x を代入して得られ，

f(x)＝a_nxⁿ＋a_n-1x^n-1＋…＋a₁x＋a₀＝0

で与えられる。これを初めの方程式の相反方程式あるいは逆数方程式という。また n 次の方程式において，その1つの根が α であれば，1/α もまたその根になる方程式のことを相反方程式ということがある。この場合，その方程式は，未知数 x の r 次の項と n－r 次の項の係数が等しい。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の相反方程式の言及

【解の公式】より

…特別な形をしているためにやさしく解けるものはある。　例　a₀Xⁿ＋a₁X^n－1＋……＋a_n＝0　(a₀≠0)において，a_i＝a_n－1(i＝0,1,2，……，n)であるとき，これを相反方程式という。(I)　nが奇数ならば－1が一つの根である。…

【高次方程式】より

…ガロアの理論によれば，方程式のガロア群が可解群であることが四則演算と根号を使って解くことができるための必要十分条件である。　2x⁴＋5x³＋7x²＋5x＋2＝0のように，n次方程式F(x)＝a₀xⁿ＋a₁x^n－1＋a₂x^n－2＋……＋a_n－1x＋a_n＝0の係数の間に，a_i＝a_n－i(i＝0,1,2，……，n)なる関係があるとき，この方程式を相反方程式と呼ぶ。nが奇数であれば，x＝－1はF(x)の根であり，F(x)＝(x＋1)G(x)と因数分解でき，G(x)＝0も相反方程式である。…

※「相反方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」