代数方程式（読み）ダイスウホウテイシキ（その他表記）algebraic equation

デジタル大辞泉

だいすう‐ほうていしき〔‐ハウテイシキ〕【代数方程式】

式がすべて代数式でできている方程式。

出典　小学館

精選版 日本国語大辞典

だいすう‐ほうていしき‥ハウテイシキ【代数方程式】

1. 〘 名詞 〙 未知数に関する代数式だけからできている方程式。⇔超越方程式。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

代数方程式 (だいすうほうていしき)
algebraic equation

多項式f（x）＝a₀xⁿ＋a₁xⁿ⁻¹＋……＋a_nに対して，f（x）＝0とおいたものを代数方程式という。多項式f（x）の次数がnのとき，n次代数方程式という。n次多項式f（x）は複素数の範囲内でf（x）＝a₀（x－α₁）（x－α₂）……（x－α_n）と因数分解できる（代数学の基本定理）。α₁，α₂，……，α_nをf（x）＝0の根という。f（x）＝0の根αがα₁，α₂，……，α_nのうちにm回現れるとき，mをαの重複度といい，m＝1であればαは単根，m≧2であればαは重根であるという。代数方程式が重根をもつかどうかはその判別式が0であるかどうかによって判定できる。

　四次以下の代数方程式はその係数から加減乗除とべき根をとる操作によって根を表すことができる。例えば二次方程式ax²＋bx＋c＝0の2根は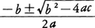，と表示できる。しかし，五次以上の一般の代数方程式は，その係数から加減乗除とべき根をとる操作によっては根を表すことができないことをN.H.アーベルは証明した。しかし，特殊な高次方程式ではその係数から加減乗除とべき根をとる操作によって根を表示できる場合もある。

　代数方程式の根のうち実数であるものを実根といい，そうでないものを虚根という。実数を係数とする代数方程式が虚根αをもてば，その共役複素数ᾱもその方程式の根である。実数を係数とするn次代数方程式f（x）＝a₀xⁿ＋a₁xⁿ⁻¹＋……＋a_n＝0の実根の分布に関してはスツルムの定理がある。多項式f（x）とその導関数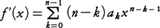，とでユークリッドの互除法を行う。ただし，その場合に剰余の符号は負にとっておく。すなわち，f（x）＝q₁（x）f′（x）－f₂（x），f′（x）＝q₂（x）f₂（x）－f₃（x），……，f_l-2（x）＝q_l-1（x）f_l-1（x）－f_l（x），f_l-1（x）＝q_l（x）f_l（x），degf_i（x）＞degf_i+1（x）（i＝0，1，……，l－1），ただし，f₀（x）＝f（x），f₁（x）＝f′（x）とおいて，f₀（x），f₁（x），……，f_l（x）を定める。例えばf（x）＝x³－9x²－3x＋1に対してはf₁（x）＝f′（x）＝3x²－18x－3，f₂（x）＝20x＋2，f₃（x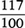）＝である。

　さて任意の実数αに対して，数列f₀（α），f₁（α），f₂（α），……，f_l（α）から0である項を除外したものの正負の符号の変わる個所の個数をV（α）とする。すると開区間（a，b）でのf（x）＝0の実根の個数はちょうどV（a）－V（b）である。これがスツルムの定理である。この定理により，区間を縮小していくことによって，実根の近似値をいくらでも精密に求めることができる。上の例のf（x）＝x³－9x²－3x＋1では，V（0）＝2，V（10）＝0であるので，区間（0，10）でf（x）＝0は実根を2個もつ。さらに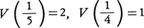，であるので，f（x）＝0は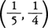に実根αをもつ。さらにV（0.2）＝2，V（0.21）＝1であるのでα＝0.20……であることがわかる。

　また実根の近似値を求める方法として，ホーナー法がある。これはf（x）＝0の実根p.qrs……の整数部分pがわかったとき，以下q，r，s，……を順次に求めていく方法である。そのために，f（x）＝b₀（x－p）ⁿ＋b₁（x－p）ⁿ⁻¹＋……＋b_nとf（x）をpを中心にして展開して方程式g（x）＝b₀xⁿ＋b₁xⁿ⁻¹＋……＋b_nを考えると，g（x）＝0は根0.qrs……をもつ。したがって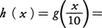b₀10⁻ⁿxⁿ＋b₁10⁻（（）ⁿ⁻¹（））xⁿ⁻¹＋……＋b_n-110⁻¹x＋b_n＝0は根q.rs……をもち，h（x）＝0の区間（0，10）内での根を調べてqを求めることができる。以下，この操作を繰り返して根p.qrs……をいくらでも精密に求めることができる。例えば，上の例の方程式f（x）＝x³－9x²－3x＋1＝0は区間（9，10）で実根βをもつ。したがってβ＝9.qrs……と書ける。このときf（x）＝（x－9）³＋18（x－9）²＋78（x－9）－26であり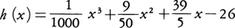，となる。h（x）は区間（3，4）内で根をもつ。したがってq＝3であり，β＝9.3……である。ホーナー法を実行するためには，実根がただ一つだけ含まれる区間をあらかじめ調べておく必要がある。これを根の分離という。

　実根の近似値を求めるのによく使われるニュートン法がある。実数aから出発して，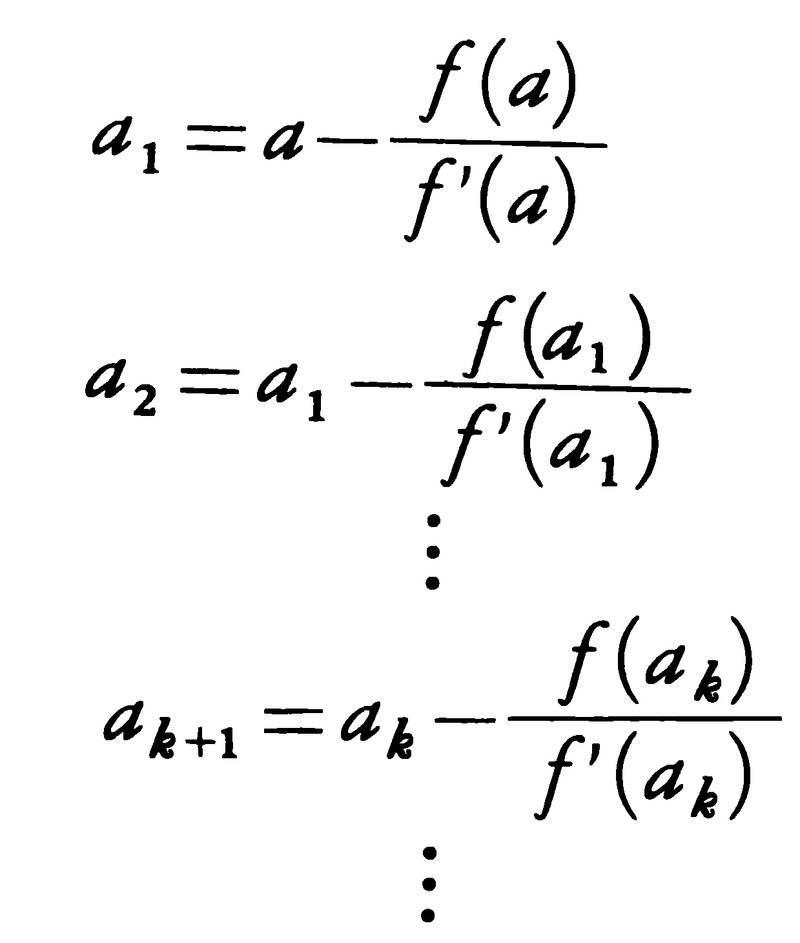

と順次a_kを定めるとき，｛a_k｝がαに収束すればαはf（x）＝0の実根を与える。a_k+1はグラフy＝f（x）の点（a_k，f（a_k））での接線のx軸との交点のx座標を与えるから，図1のような場合には｛a_k｝は実根αに収束するが，図2のような場合は｛a_k｝は収束しないかもしれず，また収束したとしてもaに近い実根に収束するとは限らない。f（x）が区間（a，b）でただ一つの実根αをもって，この区間でf′（x），f″（x）の符号が一定であれば｛a_k｝はαに収束し，a_kはαの近似を与えることが知られている。上述の例f（x）＝x³－9x²－3x＋1＝0は区間（9，10）でただ一つの根をもつ。この区間でf′（x），f″（x）はともに正であり，a＝9に対してニュートン法が適用できる。このとき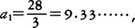a₂＝9.3107……，a₃＝9.3106……となる。一方，a＝0.2に対してニュートン法を適用するとa₁＝0.20740……，a₂＝0.207337……，a₃＝0.20733……を得る。
執筆者：上野 健爾

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

代数方程式
だいすうほうていしき

未知数x、y、z、……を含む方程式を
　　f(x,y,z,……)=0
の形で書くとき、この左辺の式が代数式（有理式あるいは無理式）である方程式を代数方程式という。

［足立恒雄］

二項方程式

X^m-a=0の形の方程式を二項方程式という。その解の一つを^m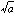またはa^1/mで表す。aが正実数のときには^m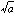は正実数とするのが普通である。

［足立恒雄］

三次方程式

三次方程式
　a₀X³+a₁X²+a₂X+a₃=0
　(a₀≠0)
を解くには、まず変数変換x=y-a₁/3a₀により
　X³+3pX+q=0…………〔1〕
の形に変形する。次に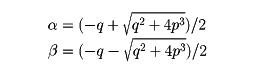

と置くと、〔1〕の解は
　　α^1/3+β^1/3,
　　ωα^1/3+ω²β^1/3,
　　ω²α^1/3+ωβ^1/3
で与えられる。ここにωは（-1+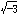）/2である。この公式をカルダーノの公式という。四次方程式は三次方程式に還元して解かれる。その解の公式をフェラリの公式という。

［足立恒雄］

代数学の基本定理

複素数体上のn次代数方程式（複素数は実数である場合を含めていう。以下同様）とは
　f(x)=a₀Xⁿ+a₁X^n-1+……
　　　+a_n-1X+a_n=0……〔2〕
　　　(a₀(≠0),a₁,……
　　　,a_nは複素数)
という形の方程式である。〔2〕の左辺の多項式はかならず
　f(x)=a₀(X-α₁)……(X-α_n)
　(α₁,……,α_nは複素数)
と一次式の積に分解できる。すなわちn次代数方程式は重複度も考慮すればn個の解を有する。これはガウスによって証明された定理で、古典代数学の基本定理とよばれる。この性質、すなわち、複素係数の代数方程式はかならず複素数解をもつという性質を、複素数体は代数的に閉じていると言い表す。たとえば有理係数の代数方程式でも、かならずしも有理数解をもつとは限らないから、有理数体は代数的に閉じていない。こういう意味から、古典代数学の基本定理は複素数体の完全性を表す一つの定理であることがわかる。

［足立恒雄］

五次以上の方程式

四次までの代数方程式はべき根を用いて、つまり、二項方程式を繰り返し解いて解を求めることができた。この性質を、四次以下の代数方程式は代数的に解けるという。

　19世紀初頭、アーベルは、五次以上の代数方程式は一般には代数的に解けないことを証明した。続いてガロアは、群の概念を導入して代数方程式が代数的に解ける必要十分条件を求めた。これが群論の始まりである。

［足立恒雄］

多元代数方程式

未知数の個数が一より多い場合は、代数方程式は平面図形や空間図形、さらには高次元図形としての意味をもつ。たとえば
　x²+y²-1=0
は円を表す。幾何学的な立場から代数方程式を研究するのが代数幾何学であり、この分野は近年著しい発達を遂げている。

［足立恒雄］

[参照項目] | 群 | 三次方程式

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

代数方程式
だいすうほうていしき
algebraic equation

ある方程式がその未知数に関して，代数式 (有理式あるいは無理式) だけから成っているとき，その方程式を代数方程式という。代数方程式は代数的な変形，すなわち加法，減法，乗法，除法，開法による変形によって，常に a₀xⁿ＋a₁x^n-1＋…＋a_n-1x＋a_n＝0 という形に書くことができるが，この方程式の根には，もとの方程式の根が必ず含まれているので，そのなかから適当な根を選んで，もとの方程式の根を求めることができる。上の方程式の指数 n に従って，もとの方程式は n 次方程式であるという。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の代数方程式の言及

【数学記号】より

…これはヨーロッパ大陸ではあまり普及せず，アメリカ，イギリスで利用された。
［代数方程式］
　ギリシアのディオファントスは方程式の未知数xとして，数を意味するギリシア語ριθμοからを取って使った。x²,x³については，平方，立方を意味する語の頭文字Δ,Kの肩にΥをつけてΔ^ΥK^Υを利用した。…

【数値解析】より

…数値解析の具体的な課題としては，問題の近似解を数値的に求めること，その近似解の性質，有効な数値計算の手順，真の値と近似解との理論的な差，丸めの誤差などの評価などである。以下では，数値解析の中の典型的な分野である，(1)行列の理論を含んだ線形代数の諸問題，(2)非線形方程式，とくに代数方程式の解法，(3)常微分方程式や熱方程式などの取扱いなどについて，考え方の例をみることにする。このほか数値積分や補間法などに現れる計算も重要な数値解析の話題になっている。…

※「代数方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」