線形常微分方程式（読み）せんけいじょうびぶんほうていしき

日本大百科全書(ニッポニカ)

線形常微分方程式
せんけいじょうびぶんほうていしき

常微分方程式のうちで未知関数とその導関数について一次式であるものを線形常微分方程式という。p(x),q(x),r(x)を区間I=(a,b)上の連続関数とし、xを独立変数、yを未知関数とする二階線形常微分方程式
　　y″+p(x)y′+q(x)y=r(x)　（1）
を考える。ここで、r(x)=0の場合の方程式
　　y″+p(x)y′+q(x)y=0 　　（2）
を同次方程式という。これに対し（1）を非同次方程式という。区間I上の関数y₁(x),……,y_m(x)は、I上でc₁y₁(x)+……+c_my_m(x)=0が恒等的に成り立つのがc₁=……=c_m=0のときに限られるとき、I上で一次独立であるといわれる。二階同次方程式（2）はI上で一次独立な解y₁、y₂をもち、（2）の一般解は
　　y=c₁y₁(x)+c₂y₂(x)
で与えられる。（2）の一次独立な解y₁、y₂を（2）の基本解系という。（2）の解y₁、y₂が基本解系であるためには、そのロンスキャン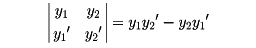

が0でないことが必要十分条件である。非同次方程式（1）の一般解は、同次方程式（2）の一般解と非同次方程式（1）の一つの特殊解の和として与えられる。（2）の基本解系をy₁、y₂とするとき、（1）の特殊解は、それをy=c₁(x)y₁(x)+c₂(x)y₂(x)と置いて、その導関数が
　　y′=c₁(x)y₁′(x)+c₂(x)y₂′(x),
　　y″=c₁(x)y₂″(x)+c₂(x)y₂″(x)+r(x)
を満たすように関数c₁(x),c₂(x)を定めることにより求められる（ラグランジュの定数変化法）。（2）でp(x),q(x)がそれぞれ定数a、bに等しいとき、代数方程式λ²+aλ+b=0を（2）の特性方程式という。この方程式が相異なる根λ₁、λ₂をもつとき（2）の基本解系はe^λ1x,e^λ2xで与えられる。また、重根λをもつときにはe^λx,xe^λxが基本解系になる。以上、二階方程式について述べたことはn階の線形常微分方程式の場合に拡張される。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)