常微分方程式（読み）ジョウビブンホウテイシキ

デジタル大辞泉

じょうびぶん‐ほうていしき〔ジヤウビブンハウテイシキ〕【常微分方程式】

独立変数が一つの微分方程式。一般的に、n階の常微分方程式にはn個の独立した任意定数（積分定数）を含む一般解が求められる。任意定数に特定の値を代入したときの解を特殊解という。

出典　小学館

日本大百科全書(ニッポニカ)

常微分方程式
じょうびぶんほうていしき

1個の独立変数をもつ未知関数とその導関数および独立変数の間に成り立つ関係式を常微分方程式という。たとえばxを独立変数、y＝y(x)を未知関数として、関係式
　　(y′)³＝27y²　　(1)
　　y″＋y＝2cosx　　(2)
　は常微分方程式である。方程式に含まれる未知関数の導関数の最高階数をその方程式の階数という。方程式が未知関数とその導関数について一次式のとき、方程式は線形であるといい、そうでないとき非線形であるという。(1)、(2)はそれぞれ1階非線形、2階線形の常微分方程式である。xを独立変数、y＝y(x)を未知関数とするとn階常微分方程式は
　　f(x, y, y′,……, y⁽ⁿ⁾)＝0　　(3)
と書くことができる。xの関数y＝(x)に対しそのn階までの導関数が定まり(3)が恒等的に満たされるとき、この関数を(3)の解という。解をすべて求めることを微分方程式を解くという。いま、c₁, c₂,……, c_nをパラメーターとする関数族y＝(x, c₁,……, c_n)が、関係式
　　F(x, y, c₁,……, c_n)＝0　　(4)
で与えられているとする。このとき(4)をxについて次々とn回微分すると、x, y, y′,……, y⁽ⁿ⁾とc₁, c₂,……, c_nに関するn個の関係式を得る。これらの関係式と(4)からc₁, c₂,……, c_nを消去すれば(3)の形の常微分方程式を得る。たとえばy－(x－c)³＝0からこの方法でcを消去すれば(1)が得られる。このことからn階常微分方程式の解は、任意の値をとる定数c₁,……, c_nを含みうることがわかる。この任意の値をとる定数を任意定数といい、n階方程式(3)に対し、n個の任意定数を含む解を(3)の一般解という。一般解が含む任意定数に特定の値を与えて得られる解を特殊解という。方程式によっては一般解が含む任意定数にどのような値を与えても得られないような解をもつことがある。このような解を特異解という。方程式(1)の一般解はy＝(x－c)³であり、y＝x³は一つの特殊解である。またy＝0はこの方程式の特異解である。方程式(2)の一般解はy＝c₁cosx＋c₂sinx＋xsinxで特異解をもたない。

　不定積分を有限回行うことにより一般解を求める方法を求積法という。特別な形の方程式に対しその求積法が知られているが、一般には求積法により常微分方程式を解くことはできない。しかし、このような場合でも一般に解をもつであろうことは次のような幾何学的考察により納得されるであろう。簡単のため一階常微分方程式
　　y′＝f(x, y)　　(5)
を考える。x、yは平面上の直交座標を表すものと考えると、(5)の解y＝(x)は平面上の一つの曲線を表す。この曲線を解曲線とよぶ。方程式(5)は解曲線上の各点(x,(x))において、この曲線の接線の方向係数′(x)がf(x,(x))に等しいことを意味する。f(x, y)により平面上の各点(x, y)において方向の場が定められているものと考えれば、解曲線を求めることは、各点における接線の方向がこの定められた方向と一致するような曲線を求めることに同値である。よって平面上の点(x₀, y₀)を与えたときこの点を通る解曲線、したがってまた
　　y(x₀)＝y₀　　(6)
を満たす(5)の解がただ一つ求まることが期待されるであろう。(6)を満たす(5)の解を求める問題を初期値問題といい、条件(6)を初期条件という。

　実際に解が存在することは、次の定理により保証される。x、yの関数としてf(x, y)は|x－x₀|≦a,|y－y₀|≦bで連続で、ある定数Mに対し|f(x, y)|≦Mであるとする。さらに適当な定数Lに対し
　　|f(x, y)－f(x, z)|≦L|y－z|　　(7)
が成り立つと仮定する。このとき初期条件(6)を満たす(5)の解が|x－x₀|≦α＝min(a, b/M)においてただ一つ存在する（コーシーの定理）。(7)をリプシッツの条件という。解の簡単な表現式がない場合でも、この定理を基礎にして解の定性的な性質を調べることが可能で、常微分方程式論として研究されている。一方、解の具体的数値（近似値）を求めるための数値計算法も開発されている。

［小林良和］

『木村俊房著『常微分方程式の解法』（1958・培風館）』▽『岡村博著『微分方程式序説』（1969・森北出版）』

[参照項目] | 線形常微分方程式

1階常微分方程式の求積法による解法

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

常微分方程式
じょうびぶんほうていしき
ordinary differential equation

微分方程式において，その未知関数が，独立変数を1つしか含まないもの (→偏微分方程式 ) 。独立変数を x とする未知関数 y＝f(x) と，この y のある階数 n までの導関数 y'，y''，…，y⁽ⁿ⁾ とから成る常微分方程式を，

F(x，y，y'，…，y⁽ⁿ⁾)＝0

と書き，これを n 階の常微分方程式という。たとえば，y''＋a²y＝0 は2階の常微分方程式である。常微分方程式はすべて，適当な変換によって1階の常微分方程式の組 (連立常微分方程式) に直すことができる。上式は，y＝y₁，y'＝y₂，y''＝y₃，…，y^(n-1)＝y_n とおけば，
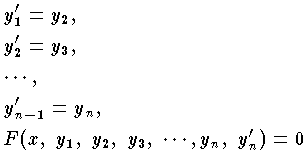のように書ける。このように1階の常微分方程式が y'_i(i＝1，2，…，n) について解かれた形 y'_i＝f_i(x，y₁，…，y_n) を，その正規形という。また一般に，n 階常微分方程式を y⁽ⁿ⁾ について解いた形 y⁽ⁿ⁾＝f(x，y，y'，y''，…，y^(n-1)) を，実の正規形という。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の常微分方程式の言及

【数値解析】より

…数値解析の具体的な課題としては，問題の近似解を数値的に求めること，その近似解の性質，有効な数値計算の手順，真の値と近似解との理論的な差，丸めの誤差などの評価などである。以下では，数値解析の中の典型的な分野である，(1)行列の理論を含んだ線形代数の諸問題，(2)非線形方程式，とくに代数方程式の解法，(3)常微分方程式や熱方程式などの取扱いなどについて，考え方の例をみることにする。このほか数値積分や補間法などに現れる計算も重要な数値解析の話題になっている。…

【微分方程式】より

…独立変数とその関数およびそれの導関数を含む方程式を微分方程式，その方程式を満足させる関数をその解と呼ぶ。微分方程式にあらわれる未知関数が1変数の関数であるとき，それを常微分方程式，多変数の関数であるとき偏微分方程式という。ここでは常微分方程式に話を限る。…

※「常微分方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」