精選版 日本国語大辞典 「導関数」の意味・読み・例文・類語
どう‐かんすうダウクヮンスウ【導関数】
- 〘 名詞 〙 ある関数 y=f (x) を微分して得られる関数のもとの関数に対する称。
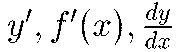 などで表わす。
などで表わす。
改訂新版 世界大百科事典 「導関数」の意味・わかりやすい解説
導関数 (どうかんすう)
derived function
数直線上の一つの区間で定義された関数y=f(x)があって,この区間に属するxに対して有限な極限値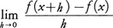 が存在するとき,関数fはxにおいて微分可能であるといい,この極限値をxにおける関数fの微分係数(または微係数,微分商)といって,
が存在するとき,関数fはxにおいて微分可能であるといい,この極限値をxにおける関数fの微分係数(または微係数,微分商)といって,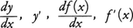 などの記号で表す。関数f(x)が区間の各点で微分可能なとき,f′(x)の値をxの関数と考えることができる。この関数f′(x)をf(x)の導関数といい,fからf′を求めることを関数fを微分するという。関数f′がまた微分可能なとき,その導関数をf″(x)で表し,これをもとの関数fの第二次導関数という。以下同様にして,fがn回微分可能なとき,fをn回微分して得られる関数を第n次導関数といい,記号
などの記号で表す。関数f(x)が区間の各点で微分可能なとき,f′(x)の値をxの関数と考えることができる。この関数f′(x)をf(x)の導関数といい,fからf′を求めることを関数fを微分するという。関数f′がまた微分可能なとき,その導関数をf″(x)で表し,これをもとの関数fの第二次導関数という。以下同様にして,fがn回微分可能なとき,fをn回微分して得られる関数を第n次導関数といい,記号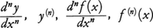 などで表す。
などで表す。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「導関数」の意味・わかりやすい解説
導関数
どうかんすう
derivative; derived function
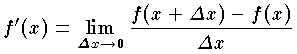 が与えられる。ここに Δx は独立変数 x の増分である。微分係数 f'(x) を x の関数と考えたとき,これを区間 [a,b] における f(x) の導関数という。 y=f(x) の導関数は f'(x) のほかに,
が与えられる。ここに Δx は独立変数 x の増分である。微分係数 f'(x) を x の関数と考えたとき,これを区間 [a,b] における f(x) の導関数という。 y=f(x) の導関数は f'(x) のほかに,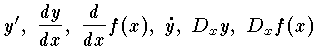 などで表わされる。区間 [a,b] において y=f(x) の導関数 f'(x) が存在するとき,この区間内の1点 x=x1 における導関数の値は,その点 x1 における f(x) の微分係数に等しい。それで微分係数を,
などで表わされる。区間 [a,b] において y=f(x) の導関数 f'(x) が存在するとき,この区間内の1点 x=x1 における導関数の値は,その点 x1 における f(x) の微分係数に等しい。それで微分係数を,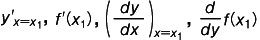 などと書く。
などと書く。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「導関数」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
日本大百科全書(ニッポニカ) 「導関数」の意味・わかりやすい解説
導関数
どうかんすう
→微分法
世界大百科事典(旧版)内の導関数の言及
【微分】より
…これらの値を調べるだけでも関数f(x)のだいたいのようすはわかるが,もっとくわしくf(x)の状態を知るためには,例えばx=aのときの〈瞬間的変化〉の状態を調べる必要が起こる。この瞬間的な変化の考えを数学的に厳密に定式化すると,すぐ後に説明するところの微分係数,導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。…
※「導関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

