ブリタニカ国際大百科事典 小項目事典 「自己準同形」の意味・わかりやすい解説
自己準同形
じこじゅんどうけい
endomorphism
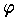を，この代数系 A の自己準同形写像という。群 G の自己準同形 
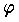とは，
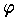が G から G 自身の上への写像 
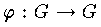であって，G のすべての元 a ，b について 
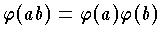が成立する写像のことである。任意の群 G の自己準同形の集合は，また一つの群をつくる。体 K の自己準同形 
とは，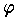
が K のそれ自身の上への写像であって，K の任意の元 a ，b に対して 
，
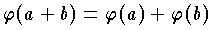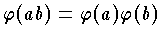が成り立つ写像のことである。体 K のすべての自己準同形は，一つの群をつくる。ベクトル空間 V の自己準同形 
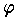とは，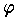
が V から V 自身の上への線形変換であって，和およびスカラー積に関する代数演算が保存される変換のことをいう。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponsored by 