乗法定理（読み）ジョウホウテイリ（その他表記）multiplication rule

デジタル大辞泉

じょうほう‐ていり〔ジヨウハフ‐〕【乗法定理】

⇒確率の乗法定理

出典　小学館

改訂新版　世界大百科事典

乗法定理 (じょうほうていり)
multiplication rule

確率論の基本的な定理。X₁，……，X_nを確率空間（Ω，F，P）上で定義された確率変数とする。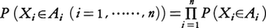が，任意のボレル集合A₁，……，A_nに対して成り立つとき，X₁，……，X_nは独立な確率変数系といわれる。この条件は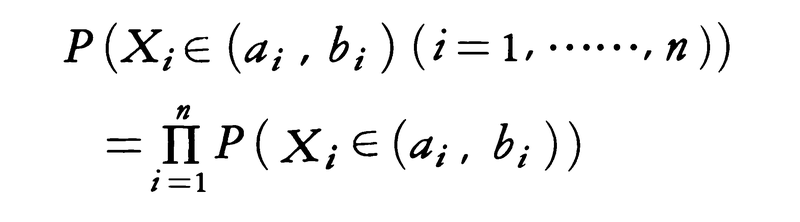

が任意のa_i＜b_i（i＝1，……，n）に対して成り立つことと同値である。確率の乗法性により，次の平均値に対する乗法定理が成り立つ。

　定理　X₁，……，X_nを独立確率変数系とする。平均値E｜X_i｜（i＝1，……，n）が有限のとき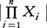の平均値も有限で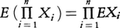，となる。すなわち，積の平均値は平均値の積になる。乗法定理により次のことが独立確率変数系X₁，X₂，……，X_nに対し成り立つ。

（1）分散の加法性　Xの分散をV（X）とかく。EX_i²＜∞（i＝1，2，……，n）のとき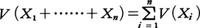，となる。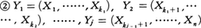とする。k_i－k_i-1次元ボレル関数f_iに対しE｜f_i（Y_i）｜＜∞（i＝1，2，……，j）ならば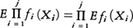，が成り立つ。
執筆者：西尾 真喜子

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

乗法定理
じょうほうていり

→条件つき確率

出典　小学館　日本大百科全書(ニッポニカ)