確率（読み）カクリツ（英語表記）probability

デジタル大辞泉

かく‐りつ【確率】

《probability》ある事象の起こる可能性の度合い。公算。蓋然率がいぜんりつ。「確率が高い」
[類語]公算・蓋然的・蓋然性・可能性・プロバビリティー

出典　小学館

精選版 日本国語大辞典

かく‐りつ【確率】

1. 〘 名詞 〙 ( [英語] probability の訳語 ) ある事象が起こる確からしさの度合い。また、それを示す数値。蓋然率(がいぜんりつ)。公算。
   1. [初出の実例]「各子音がそれぞれ各国語に出現する頻度あるいは確率が一様で」(出典：比較言語学に於ける統計的研究法の可能性に就て（1928）〈寺田寅彦〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

確率 (かくりつ)
probability

銅貨を投げて表が出たり裏が出たりするのは同じ程度に期待できるとか，明日は雨がほとんど降ることはなかろうなど，偶然に支配されて起こる事柄について，それが起こる可能性の大小を表す数値が確率である。そしてそのような現象を数学的に取り扱うのが確率論である。実際の具体的な現象では偶然に起こる事実に加えて他のいろいろな要因が関係してきて複雑になるので，理想化したモデルを想定して考えることが多い。それにしても，偶然とかでたらめの中にある法則を見つけて推論を進めていくだけに，確率の取扱いには厳密な議論が必要となる。

　確率の概念が数学の中に定着してきたその歴史は浅いが，確率論は数学の他の分野や物理学をはじめとする自然科学の諸分野と密接に関連しあって，最近急速に発展してきた。数学としての確率論の起りは，17世紀にフランスのB.パスカルとP.deフェルマーによる賭の考察，さらにそれに刺激されてゲームについての書物も著したオランダのC.ホイヘンスらの業績にあったといってよかろう。また同じころ，イギリスのJ.グラウントによる生命表の作成などの統計的研究も確率論の発生を促したとされる。次いで18世紀に入り，ヤコブ・ベルヌーイの遺稿が，甥のニコラウスによってまとめられ，《推測法》（1713）として出版されたが，そこには順列・組合せを用いた確率の話が出てきて，しだいに確率論としての形態を整えてきたのであった。

　ここでも創生期のように有限個の事象を扱った確率から話を始める。例えば，銅貨を投げるとき，それがゆがんでいないなら表の出る確率と裏が出る確率が同じであるとしてよかろう。そのとき表の出ることと裏が出ることをそれぞれ一つの事象と考え，それらの事象の確率が1/2であるとする。もう少し自明でない例をあげよう。

　例1　同じ形の4枚の字札a，b，c，dがある。これらを1列に並べるとき，どの順列（順序を考慮した配列）もえこひいきなく同じ程度に起こりうるとすれば，かってに並べる操作は偶然現象と考えられる。並べ方は全部で4！＝4×3×2×1＝24通りあるので，ある特定の並べ方，例えばa，b，c，dの順に並べられる確率は1/24である。またaが最初に並ぶような場合は3！＝6通りあるので，そのような事象の確率は6/24＝1/4となる。同様にbが最初に並ぶ，cが最初に並ぶ，そしてdが最初に並ぶ確率はすべて1/4となり，公平な並べ方をしている立場から，期待どおりの結果が得られる。

　この例のように，全体でn通りの可能性があって，どれもが同じ程度に期待できる（あるいは起こりやすい）とする。このとき指定された条件にあう場合がm通りなら，その条件が満たされる確率pは，

　p＝m/n

と定義される。またn通りある個々の場合を根元的な素事象と考え，根元事象と呼ぶ。例1の場合でいえば一つの順列が根元事象となる，いくつかの根元事象からなる集合を事象と呼ぶ。それがm個からなれば，この事象の確率が上記p＝m/nとなるのである。

　より進んだ確率論を展開するには，同じ考え方ではあるがもっと一般的な定義に拡張しておく必要がある。そのようなものとして，1933年にソ連のA.N.コルモゴロフによって提唱された公理系がある。根元事象をωとかき，それらの全体をΩとする。取り扱いたい事象（Ωの部分集合）の集合をBとする。このBは和集合や補集合をとる演算に関して閉じていることが要請される。すなわち，Bに属している事象A₁，A₂，……があればその和事象A₁∪A₂∪……もBの要素となること，およびBに属するどんな事象Aに対しても，その補集合A^c＝Ω－AもまたBに属するものとする。A^cは事象Aの余事象と呼ばれる。なお，全事象ΩはBの要素になっているものとする。

　また，（1）Bの各事象Aに対してその確率と呼ばれる数P（A）が対応していて，0≦P（A）≦1，（2）全事象ΩについてはP（Ω）＝1，さらに（3）Pは次の完全加法性を満たすとする。事象A，Bの共通集合が空であるとき両者は排反であるというが，いま排反事象の列A₁，A₂，……が与えられたとしよう。このとき和事象A＝A₁∪A₂∪……の確率は各事象の確率の和に等しい。すなわち，

　P（A）＝P（A₁）＋P（A₂）＋……

　こうした性質をもつ組（Ω，B，P）を確率空間と呼び，数学的な議論が展開される場となる。ここでPは解析学で測度といわれているものにほかならないが，P（Ω）＝1となる特別な測度である。

　例2　二つのさいを投げたとき，目の出方は6×6＝36通りある。出た目の数の組を（1，1），（1，2），……，（2，1），（2，2），……，（6，6）と記し，それらおのおのを根元事象とみる。全体をΩとし，BとしてはΩの部分集合のすべてからなるもっとも詳しいものをとる。事象A（∈B）の確率はP（A）＝♯（A）/36とする。ただし，♯（A）はAに含まれる根元事象の個数を表す。例えば出た目の和が4となる事象は（1，3），（2，2），（3，1）の組からなり，その確率は3/36＝1/12である。

　この例で，第1のさいの出る目が1である事象Aは（1，1），（1，2），……，（1，6）からなり，第2のさいの出る目が3である事象Bは（1，3），（2，3），……，（6，3）からなる。A∩Bはただ一つの根元事象（1，3）でその確率は1/36となる。P（A）＝P（B）＝6/36＝1/6に注意すれば等式，

　P（A∩B）＝P（A）P（B）

が成り立つ。このような場合，AとBは独立であるといい，A，Bは独立事象という。また例1では，例えばaがbより前に並ぶ事象とcがdより前に並ぶ事象とは独立になる。多数の事象A₁，A₂，……があるとき，それらからいくつかかってに選んだA_i，A_j，……，A_kについて，つねに，

　P（A_i∩A_j∩……∩A_k）＝P（A_i）P（A_j）……P（A_k）

が成り立つとき，もとの事象の系は独立であるという。

試行

さいを投げる場合のように，結果が偶然的なもので排反事象の列A₁，A₂，……で表されるとし，それらのうちのどれか一つが必ず起こる，すなわちP（A₁）＋P（A₂）＋……＝1であるときこれを試行という。さいを投げる場合なら等しい確率の6個の排反事象が，銅貨なら二つの排反事象が対応する。いま二つの試行をとりあげ，これらをT₁，T₂とかく。両者にはそれぞれ排反事象の列A₁，A₂，……とB₁，B₂，……が対応しているとしよう。もし，かってに選んだA_iとB_jが独立，すなわちP（A_i∩B_j）＝P（A_i）P（B_j）ならば試行T₁，T₂は独立であるという。さいや銅貨を二度投げる場合はこれにあたる。このような独立な試行は何回も繰り返すことができる。とくに毎回同じ試行がなされ，しかも2種類の実現の可能性しかないとき，これをベルヌーイ試行という。対応する排反事象は二つのみで，A₁およびA₂（＝A₁^c）である。それらはそれぞれ成功，失敗と呼ばれ，確率をpおよびq（＝1－p）で表すことが多い。

条件付き確率

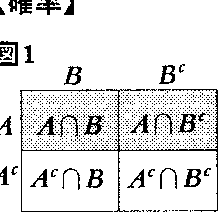
二つの事象A，Bがあるとき，両者の関係は次の4通りが考えられる。（1）AとBが起こる（図1），（2）Aが起こりBが起こらない，（3）Aが起こらずBが起こる，（4）AもBも起こらない。余事象A^c，B^cを使って上の各場合を事象で表せば，それぞれ，（1）A∩B，（2）A∩B^c，（3）A^c∩B，（4）A^c∩B^cとなる。いまAが起こった場合を考えよう。可能性としては（1）と（2）の場合だけとなり，それがすべてである。そこで視点をかえてAを全事象と考えることにすれば，そこでBおよびB^cの占める割合は，それぞれP（A∩B）およびP（A∩B^c）に比例するので，全事象の確率を1とすることに注意すれば，Aが起こったときのB，B^cの条件付き確率は，

　P_a（B）＝P（A∩B）/P（A），

　P_a（B^c）＝P（A∩B^c）/P（A）

とすればよい（当然P（A）＝0のときを除く）。この記号を用いれば，Aが起こり続いてBが起こる確率，すなわちP（A∩B）はP（A）P_a（B）に等しい。

　三つの事象A，B，Cがあるとき，P_a（B），P_b（C）などだけでなく，AとBが起こったときのCの条件付き確率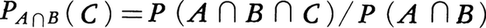などが定義される。事象A，B，Cがこの順に起こったとすれば，等式P（A∩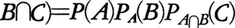は，まずAが起こり，Aが起こったという条件のもとでBも起こり，さらにAもBもともに起こったという条件のもとでCも起こったというように説明される。

　例3　壺の中に同じ大きさの球が40個入っている。そのうち14個は赤色に，26個は青色に塗ってある。これらの球は重いものと軽いものの2種類の材質のどちらかでできており，赤球は8個が，青球は10個が重い（図2）。壺が暗室の中にあり，手探りで重い球を一つとり出したとき，それが赤球である確率は（赤くて重い確率）/（重い確率）＝（8/40）/（18/40）＝4/9である。また明るいところで球にふれることなく赤球を一つ選び，それが重い球である確率は（赤くて重い確率）/（赤い確率）＝（8/40）/（14/40）＝4/7である。これらの確率は，40個の根元事象からなる確率空間において，それぞれ重い球を選んだ，および赤球を選んだという条件下での赤球および重い球が選ばれる条件付き確率となっている。

　排反事象の列H₁，H₂，……，H_nがあって，その和が全事象になるとする。任意の事象Aに対して，関係式P（A）＝P（A∩H₁）＋P（A∩H₂）＋……＋P（A∩H_n）と，P（A∩H_i）＝P（A）P（H_i/A）＝P（H_i）P（A/H_i）を用いてP（A∩H_i）/P（A）をかき直せば，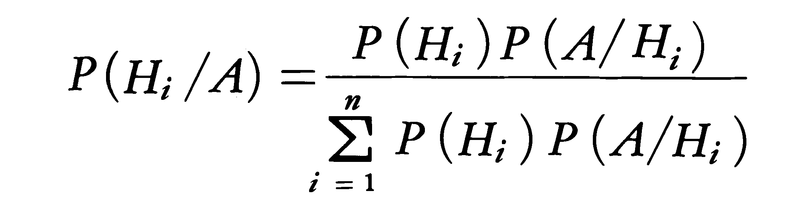

が得られる。これがいわゆるベイズの定理である。

　条件付き確率の特別な場合として，事象AとBが独立な場合のP_a（B）を考えよう。P（A∩B）＝P（A）P（B）だから，P_a（B）＝P（B）となる。同様にP_b（A）＝P（A）も正しい。三つの事象A，B，Cが独立であるとき，P_ab（C）＝P（C），P_bc（A）＝P（A），P_ca（B）＝P（B），またP_a（B）＝P（B）だからP（A∩B∩C）＝P（A）P（B）P（C）が成り立ち，独立性の定義における一つの式と一致する。

　ここで事象の和についての公式も出しておこう。P（A∪B）＝P（A）＋P（B）－P（A∩B），P（A∪B∪C）＝P（A）＋P（B）＋P（C）－P（A∩B）－P（B∩C）－P（C∩A）＋P（A∩B∩C）は図3より容易にわかる。より一般に，事象A₁，A₂，……，A_nについては，P（A_i）＝P_i，P（A_i∩A_j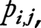）＝……、P（A₁∩A₂∩……∩A_n）＝P₁₂、……、_n とおいて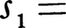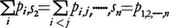，とすれば，

　P（A₁∪A₂∪……∪A_n）＝s₁－s₂＋……＋（－1）ⁿ⁻¹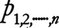

となる。左辺はどれか少なくとも一つのA_iが起こる確率である。

順列，組合せ

有限個の根元事象からなる場合，事象の確率を求める問題は，順列や組合せの数を数えることに帰着される場合が多い。例1の4文字を並べる場合，どの並べ方も同じ程度に起こりやすいとしたから，問題の条件にあう並べ方が何通りかというのは順列の問題にほかならない。この事情は文字の個数が増えても同様であって，基本的な計算には，異なるn個のものからr個とって1列に並べる方法が全部で，

　_nP_r＝n（n－1）（n－2）……（n－r＋1）＝n！/（n－r）！

だけあることが用いられる。

　毎回，成功する確率がp（0＜p＜1）であるn回のベルヌーイ試行を考える。n回のうちk回成功（したがってn－k回失敗）だとすれば，可能性としては成功したk回がどの試行であったかその経過を指定する方法だけある。それはn個からk個をとる組合せの数_nC_k＝_nP_k/k！に等しい。そしておのおのの確率は，独立な試行の結果であるためp^kqⁿ⁻^kである（q＝1－p）。よって，とにかくk回成功する確率は，組合せを用いて_nC_kp^kqⁿ⁻^kであることがわかる。

確率変数と確率分布

n回のベルヌーイ試行で成功する回数をXと書けば，それは偶然によっていろいろな数値をとる変数である。このような変数を確率変数という。一般に確率変数とは，それがとる値のそれぞれに一定の確率が付与されているような変数であるということができる。したがって，確率空間の言葉を用いれば，それは根元事象ωの関数X（ω）で，すべてのxについてX（ω）≦xとなるようなωの全体が事象，すなわちBの要素でありその確率が定まるようなものである。そのような確率を簡単にP（X≦x）とかく。前記のベルヌーイ試行の場合はX＝kとなる確率が求まり，前述のようにP（X＝k）＝_nC_kp^kqⁿ⁻^kである。一般にXのとる値がx₁，x₂，……のように離散的な値に限るときには，Xは離散形確率変数といい，P（X＝x_k）＝p_kで定義される数列｛p_k｝をXの分布という。また，関数F（x）＝P（X≦x）はXの分布関数と呼ばれる。Xが離散形確率変数の場合には分布関数は階段関数となる（図4）。これとは対照的に分布関数F（x）が絶対連続，すなわち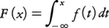と表されるとき，Xは連続形であるといい，f（x）を密度関数と呼ぶ。

　離散形の場合に戻って分布の例をあげよう。

　例4　Xをn回のベルヌーイ試行で成功する回数を表す確率変数とする。そのとる値は0，1，2，……，nで分布｛p_k;0≦k≦n｝はp_k＝_nC_kp^kqⁿ⁻^kである。これを二項分布という。これは重要な離散形分布の例で，応用上もよく現れる。例えば電話による業務を主体とする事業所があって，従業員は12名，各人は独立に行動し1時間の間に平均して20分の割合で電話を使用しているものとしよう。電話器は何台用意したらよいであろうか?　ある時刻をとって，電話中であることを成功とみることにすれば，nが12のベルヌーイ試行でp＝20/60＝1/3の場合と考えられる。統計数値表によればp₇＋p₈＋……＋p₁₂＝0.0664……程度となり，電話器を6台常備すれば不つごうが生ずることは7%以下の確率となる。

　例5　離散形確率変数のもう一つの重要な例はポアソン分布に従うものである。分布｛p_k;k≧0｝はp_k＝（λ^k/k！）e⁻^λ（λ＞0）で与えられる。この分布が現れる具体例は多い。

　例6　ガウス分布（正規分布）は連続形の分布で密度関数が次式で与えられる。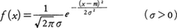

これはいろいろな意味でもっとも重要な分布で，まさに分布の中の王座を占めるものである。

　このように，確率がどのように散らばるかが分布によって示されるが，その全体を把握するのは一般に容易でない。そのため一つの数値で分布の特性量を表すことができれば好つごうである。重要な特性量としては，平均値（期待値ともいう）と分散がある。離散形の場合なら平均値mは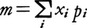，で，分散σ²は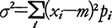，で与えられる。分散の平方根σ（＞0）が標準偏差で散らばりの程度を表す。連続形のときも平均値，分散が類似した式で定義される。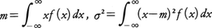

　これまで，確率変数によって確率が分布するようすを見たが，これを発展させて多次元の確率変数を考えたり，また時間のパラメーターを入れて確率過程を導入したりして，確率論としての学問体系が築かれ，現代数学の一分野として発展していくのである。
執筆者：飛田 武幸

図－確率

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

確率
かくりつ
probability

「今日、東京で雨が降る確率」「A君がB大学に合格する確率」「A大学がリーグ戦で優勝する確率」「今後10年のうちに東京地区で大地震が起こる確率」というように、確率ということばはいろいろな場面で使われている。簡単にいえば、確率は確からしさの程度を0と1との間の数値として表したもので、確からしさの程度が高いとき1に近く、低いとき0に近い。また確率が0.3であることを確率は30％というように、パーセンテージで表すこともある。始めにあげたいくつかの例の場合に、その確率として一つの数値を具体的に正確に定めるのは容易なことではないし、またそれほど意味のあることでもない。これらの例の場合には5％未満とか、ほぼ50％とか90％とかの程度で十分であろう。

　さて、偶然的に起こるある事柄が実際に起こる確率をどのように定めるか？　同一条件のもとで繰り返して実験ができる場合には、相対度数（N回の繰り返しのうち実際に起こった回数がnであったときn/Nを相対度数という）の値の極限（繰り返しの回数を大きくしたときの）として確率を定めることができる。ただし実際には繰り返しの回数は有限であるから、具体的には近似的な値が定まるだけである。実験を繰り返し行わなくても確率が一定値をとることが期待される場合もある。たとえば、コインを投げたとき表の出る確率は1/2、さいころを投げたとき6の目の出る確率は1/6などである。

［古屋　茂］

同様に確からしいこと

さいころを投げたとき、どの目が出るのも同じ確からしさをもつと考えられる。ラプラスは「同様に確からしい」という先験的判断に基づいて確率を定義した。すなわち、結果が偶然に支配されるような実験や観察において起こりうる結果が全部でn通りあり、これらのうちのどれが起こるかが「同様に確からしい」ものとする。このとき着目する事柄Aが起こるのがn通りのうちのa通りであるとすると、Aの起こる確率をa/nと定める。たとえば、さいころを投げたとき6の目の出る確率は1/6であり、偶数の目が出る確率は3/6すなわち1/2である。

　何を「同様に確からしい」と考えるかによって確率が別々な値をとることがある。その例をあげよう。

　図Aのような道を通って、AからBまで回り道をしないで行くとする。Cを通る確率を求めてみる。

〔解(1)〕AからBへ回り道をしないで行く方法は、4から2をとる組合せ、すなわち₄C₂＝6通りある。一方、Cを通る方法は2×2＝4通りあるから、6通りのうちの4通り、すなわち4/6＝2/3が求める確率である。

〔解(2)〕AからBへ向かうとき、A、D、C、Eの4点ではどちらへ進むか二つのうちの一つを同じ確からしさで選ぶことにする。このときDからCへの道を通る確率は(1/2)×(1/2)＝1/4であり、同じくEからCへの道を通る確率も1/4であるから、Cを通る確率は1/4＋1/4＝1/2となる。

　この二つの解答のどちらが正しいか。AからBへの6通りの道のどれを選ぶかが「同様に確からしい」ときは解(1)が正しい。またA、D、C、Eの各点でどちらへ進むかその選び方が「同様に確からしい」ときは解(2)が正しい。この問題をことばどおりに解釈すると、解(2)のほうが解(1)よりも自然な考え方のように思われる。

　場合の数に関連する確率の問題では、何が「同様に確からしい」かを明確にすることが重要であって、このような確率の問題を考えるとき、「同様に確からしい」場合にまで場合を分解して考えることがたいせつである。「三つのさいころを同時に投げると、目の和が9になる場合の数と、目の和が10になる場合の数とは同じはずであるのに、実際は和が10になるほうが起こりやすいのはなぜか」と友人に尋ねられたガリレイは、(1,2,6)、(1,4,4)、(3,3,3)の起こり方はそれぞれ6通り、3通り、1通りであることに注目し、目の和が9になるのは6×6×6＝216通りのうちの6＋6＋3＋3＋6＋1＝25通り、目の和が10になるのは6＋6＋3＋6＋3＋3＝27通りであるので、和が10になるほうが起こりやすいと解答を与えたという。このようにガリレイは「同様に確からしい」場合にまで分解して考えたから正しい結果が得られたのである。

［古屋　茂］

確率論の歴史

17世紀のなかばごろにおけるパスカルとフェルマーの文通で取り上げられたいくつかの話題が確率論の始まりといわれているが、それ以前にもガリレイが確率の問題を考えている。パスカル、フェルマーが興味をもったのは、本質的には場合の数を求める問題であった。1657年に出版されたホイヘンスの『さいころ遊びの理論について』は、14の命題からなっているが、そのなかには、さいころについて確率論的に考察したものが含まれている。ベルヌーイはその死後刊行された『推論法』Ars Conjectandi（1713）において、ホイヘンスの研究結果を一般化し、順列・組合せ理論を系統づけ、また初めて大数(たいすう)の法則を定式化してその証明を与えている。以後多くの数学者が確率について論ずるようになったが、ラプラスは1812年に『確率の解析的理論』を完成した。これは、当時、目覚ましい発展を続けていた解析学を武器とし、新しい手法を導入して、それまでの確率の知識を集大成したものである。このラプラスの業績は以後の研究の出発点ともなり、確率の考えは多くの分野で効果的に応用されるようになった。とくに統計学においては確率は欠くことのできないものとなった。19世紀までの確率論を古典確率論とよぶこともある。

　20世紀になって確率論は大きく飛躍した。ボレルは、区間(0,1)の実数を二進展開したとき、ほとんどすべての実数に対して（すなわち測度0の集合に属する実数を除いて）n位までに現れる1の相対度数がn→∞のとき1/2に近づくことを示した。またルベーグは、ジョルダンによる測度論およびボレルによる測度論の両方を特別の場合として含むような一般的な測度論をつくりあげた。この測度の理論は確率論にも大きな影響を与え、1933年にコルモゴロフは、ルベーグ式測度に基づく確率論の公理系を提示して数学としての確率論が確立された。これは測度論的確率論ともよばれている。この測度論的方法は、古典的確率論では手がつけられなかった問題（たとえば確率過程の問題など）に対しても有力であって、現在も急速に発展しつつある。測度論的確率論の基本的部分の公理系は集合と測度のことばを使って書かれている。測度理論に詳しくない読者にもその内容の大筋だけは理解できるように、次にまず、確率についての公理的考えを簡単な場合について説明しておく。

［古屋　茂］

公理的方法による確率論

ラプラスは「同様に確からしい」という概念を基にして確率を定義した。カードやさいころなど、場合の数に関連する問題に対してはこれで十分であろう。しかし、確率が応用される範囲が拡大されてくると、「同様に確からしい」という判断が不可能になる場合も生じる。そこで相対度数を基にした確率も考えられるようになった。この方向を代表するものはミーゼスの確率論である。確率の意味そのものについてはいろいろな考え方がある。しかしどのような意味づけをしようとも、確率としてもつべき共通の基本的性質があるはずである。確率とは何かというような問題から離れて、確率のもつ基本的な性質を抜き出し、それだけを基にして、すなわち公理系を基にして確率論を構成するのである。ここでは、ある偶然的な事柄で起こりうる場合の数が有限個である場合を考える。

　結果が偶然に支配されるような実験または観測を試行ということにする。たとえば、さいころを投げるのは一つの試行である。ある試行において起こりうる結果の全体をω₁、ω₂、……、ω_nで表すとき、集合
　　Ω＝｛ω₁,ω₂,……,ω_n｝
をその試行の標本空間という。たとえば、さいころを投げる試行においては標本空間は6個の元(げん)をもつ。また硬貨を2回投げて表・裏を調べる試行においては、標本空間は
　　(表,表)，(表,裏)，(裏,表)，(裏,裏)
の4個の元よりなる。

　標本空間Ωの元を根元事象といい、Ωの部分集合を事象という。事象Aが起こるというのは、試行の結果を表すω（Ωの元）がAの元であることを意味する。二つの事象A、Bに対してA∪B、A∩BをそれぞれA、Bの和事象、積事象という。Ā＝Ω－AをAの余事象、Ωを全事象、∅（＝空集合）を空事象という。

　A∩B＝∅のとき、二つの事象A、Bを排反事象という。これはAとBがともに起こることがないことを表している。たとえば、5本のくじのうちに2本の当たりくじがあるとする。このくじをまずAが、次にBが引くという試行について次のような問題を考える。

　①この試行の標本空間をつくれ。②Aが当たるという事象はこの標本空間のどんな部分集合か。③Bが当たるという事象はこの標本空間のどんな部分集合か。

　これを解くために5本のくじを1、2、3、4、5で表し、1と2が当たりくじとする。A、Bが引いたくじをそれぞれa、bで表せば、試行の結果は(a,b)(a≠b)で表される。したがって標本空間は図Bのような20個の元よりなる。次にAが当たるという事象は図で上の2行の8個の元よりなる。またBが当たるという事象は左の2列の8個の元よりなる。

　Ωの部分集合全体を定義域とする関数Pが
(1)任意の事象Aに対してP(A)≧0
(2)P(Ω)＝1, P(∅)＝0
(3)A∩B＝∅のときP(A∪B)＝P(A)＋P(B)
を満たすとき、Pを確率といい、P(A)を事象Aの起こる確率という。根元事象が「同様に確からしい」とき、Ωの元の個数をn、Aの元の個数をaとすれば
　　P(A)＝a/n
となる。

　前のくじの例では、根元事象は「同様に確からしい」と考えられるから、初めにくじを引くAが当たる確率も、次に引くBが当たる確率も同じ値の2/5となる。まったく同じ方法でn本のうちr本の当たりくじがあるとき、初めにくじを引く人も、次に引く人も、当たる確率は同じであることが示される。

［古屋　茂］

測度論的確率論

確率空間、事象、確率

空集合でない集合Ωが与えられている。Ωの部分集合を元とするある集合族（は集合を元とする集合であるから集合族とよぶ）があって、次の三つの条件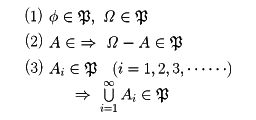

が成り立つとき、集合族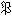をΩにおける完全加法族という。

　集合ΩとΩにおける完全加法族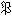が与えられたとき、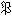で定義された実数値関数Pが次の条件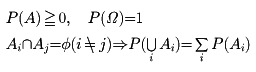

を満たすとき、Pを(Ω,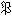)上の確率測度または確率分布という。このときΩを標本空間、Ω、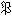、Pをまとめたもの(Ω,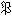,P)を確率空間という。Ωの元を標本点または根元事象とよぶ。なお、Ωの部分集合全体の集合は完全加法族をなすことは明らかであるが、ここで問題とする集合族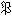は一般にΩの部分集合全体からなる集合族ではない。測度論のことばでいえば、可測でない集合は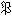には属さない。この点は前に述べた標本空間が有限集合の場合と異なっている。

　集合族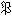の元を事象といい、P(A)を事象Aの確率という。∅（空集合）を空事象、Ωを全事象という。事象A、Bに対してA∪B、A∩Bをそれぞれ和事象、積事象とよぶ。事象Aに対してĀ＝Ω－AをAの余事象という。二つの事象A、Bに対してA∩B＝∅のときA、Bは排反事象であるという。

［古屋　茂］

事象の独立

二つの事象A、Bが独立であるとは
　　P(A∩B)＝P(A)P(B)
が成り立つ場合をいう。一般にn個の事象A₁、A₂、……、A_nが独立であるとは、任意の
　　1≦i＜j＜……＜k≦n
に対して
　　P(A_i∩A_j∩……∩A_k)
　　　＝P(A_i)P(A_j)……P(A_k)
が成り立つ場合をいう。

［古屋　茂］

確率変数、分布関数

確率空間(Ω,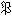,P)を考える。Ωで定義された実数値関数Xについて、任意の実数aに対して｛ω|X(ω)＜a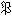｝∈が成り立つとき、Xを確率変数という。Ωを実数全体の集合Rとし、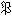¹をRにおけるボレル集合の全体とする。

　確率変数Xに対して
　　Φ(A)＝P(ω|X(ω)∈A) (A∈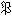¹)
と置けば、Φは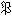¹上の確率分布となるが、このΦをXの確率分布という。実数aの関数
　　F(a)＝P(ω|X(ω)≦a)
をXの分布関数という。

　n個の確率変数X₁、X₂、……、X_nに対してX_iを第i成分とするベクトルX＝(X₁,……,X_n)をn次元確率変数という。このとき、n変数の関数
　　F(a₁,a₂,……,a_n)＝P(ω|X₁(ω)≦a₁,
　　　X₂(ω)≦a₂,……,X_n(ω)≦a_n)
をXのn次元分布関数という。

［古屋　茂］

確率変数の独立性

有限個の確率変数X₁、X₂、……、X_nが与えられたとき、任意の一次元ボレル集合A_i(1≦i≦n)に対して
　　P(ω|X₁(ω)∈A₁,……,X_n(ω)∈A_n)
　　　＝P(ω|X₁(ω)∈A₁)……P(ω|X_n(ω)∈A_n)
が成り立つ場合に、X₁、X₂、……、X_nは互いに独立であるという。

［古屋　茂］

確率変数の平均値、分散、標準偏差

確率変数Xに対して、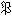上の測度Pによるルベーグ積分が考えられXがPに関して積分可能であれば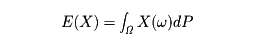

をXの平均値という。XがPに関して積分可能でなければXの平均値は存在しない。また、(X－E(X))²が積分可能のとき
　　V(X)＝E((X－E(X))²)
をXの分散といい、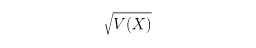

をXの標準偏差という。次の関係が成り立つ。

　　E(aX＋bY)＝aE(X)＋bE(Y)
X、Yが独立であれば
　　E(XY)＝E(X)E(Y),
　　V(X＋Y)＝V(X)＋V(Y)
［古屋　茂］

共分散と相関係数

二つの確率変数X、Yに対して
　　C(X,Y)＝E((X－E(X))(Y－E(Y)))
の右辺が存在するとき、C(X,Y)をX、Yの共分散という。とくに、X、Yが独立であればC(X,Y)＝0である。また、X、Yの分散が存在するとき
　　V(X＋Y)＝V(X)＋V(Y)＋2C(X,Y)
が成り立つ。

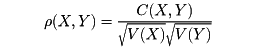
を、X、Yの相関係数という。次式が成り立つ。

　　|ρ(X,Y)|≦1
X、Yが独立であれば相関係数は0であるが、相関係数が0であってもX、Yは独立でないこともある。

［古屋　茂］

『伊藤清著『確率論の基礎』（1944・岩波書店）』▽『伊藤清著『現代数学14　確率論』（1953・岩波書店）』▽『河田敬義著『確率論』（1948・共立出版）』▽『W・フェラー著、河田竜夫・国沢清典監訳『確率論とその応用　Ⅰ上下　Ⅱ上下』（1960～1970・紀伊國屋書店）』

[参照項目] | 順列・組合せ | 測度 | 大数の法則

確率（同様に確からしいこと）〔図A〕

確率（公理的方法による確率論）〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

確率
かくりつ
probability

ある物事が起るか起らないかが確実に知られていないとき，その物事が起る確からしさ，つまりどのくらいの割合で起るかを表わす値を確率という。それが確実に起るときは確率は1であり，起らないことが確実ならば確率は0である。多数の物事があるとき，1つの試行で同時には起りえない事象を排反事象，最小単位の排反事象を基本 (根元) 事象といい，基本事象の全体の集合を全事象という。確率の値はそれらの事象の生起に関する経験的知識によって決る。なんらの経験もないとき，どの基本事象も等しい可能性で起ると仮定すれば，事象A が起る確率は
で与えられる。これを先験的確率という。ところが，たとえば，サイコロが完全に均質ならばどの目も等しい可能性で出るかもしれないが，少しでも不均質ならば特定の目が出やすいかもしれない。 R.ミーゼスは古典的確率の等可能性は等確率という意味以外に理解しようがなく，循環論的であると非難し，確率を観測系列における相対度数の極限として定義することを提唱した。すなわち，N₁ 回の試行のなかで事象Aが起る度数を R₁ 回とし，このような試行の回数を逐次増して N₂ 回，N₃ 回，…の試行では生起の度数が R₂ 回，R₃ 回，…であるとすれば確率 Pr(A) を試行回数が無限に増したとき i→∞ の Ri/Ni の極限として定義する。これを経験的確率という。さらに A.N.コルモゴロフは，確率の基本的性質に着目し，確率を適当な公理系を満足する量と考えて測度論的な方法で論理的に確率論を展開した。このように定義された確率を測度論的確率という。以上の確率の考察では，試行の繰返し可能性が大前提になっている。自然現象や社会・経済現象の集団を統計的に研究する推測統計学に確率の考えを適用するとき，繰返し可能な現象では経験的確率は受入れやすい考え方である。しかし，必ずしも繰返し可能でない事象に対しても確率を考えたいときがある。そのような場合に対し，J.M.ケインズは2つの命題の間の論理関係について確率を定義しようとする考えを提唱した。この考え方は H.ジェフリーズによって体系づけられたもので，論理的確率と呼ぶこともある。 L.J.サベジや B.ド・フィネッティは，この立場から統計的決定や統計的推測の問題を考えた代表者である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

確率【かくりつ】

ある事象の起こり得る可能性を数で表したもの。過去の頻度(ひんど)数から推定する経験的（統計的）確率と数学的確率とがある。確率の数値は１より小さく，負でない。一般に，一つの集合Ωの部分集合E（事象）に数P（E）を対応させたとき，a.0≦P（E）≦１，b.P（Ω）＝１，c.部分集合A，Bが共通部分をもたないときはP（A＋B）＝P（A）＋P（B），の三公理が成立すれば，P（E）をEの確率という。→確率誤差
→関連項目加法定理｜大数の法則｜排反事象｜無作為抽出

出典　株式会社平凡社

ASCII.jpデジタル用語辞典

確率

ある事象が起こる割合をいう。すべての事象が起こる確率がすべて等しい場合には、それらの場合の数を計算してその逆数を求めれば、それが当該事象が起こる確率となる。

出典　ASCII.jpデジタル用語辞典

栄養・生化学辞典

確率

　ある事象が何種類かの仕方で起こる場合，そのうちの一つもしくは複数の仕方が起こる割合を示す数値，もしくはそれを予測させる数値．

出典　朝倉書店

世界大百科事典（旧版）内の確率の言及

【パスカル】より

…しかしこの間メレA.G.chevalier de Méréなどの社交界の人士との交友を通じて，人と人との自然で節度ある交わりを理想とする〈オネットムhonnête homme(紳士，教養人)〉のあり方に開眼し，〈幾何学的精神〉とは異なる〈繊細の精神〉で人間を観察することを学ぶ。同時に科学研究も精力的に続行し，〈大気の重さ〉と〈流体の平衡〉に関する論文を仕上げ(刊行1663)，さらに賭博の賭金の分配のしかたをめぐってメレから受けた質問に端を発してフェルマーとともに確率の問題を論じ，その成果として《数三角形論》(刊行1665)を著した。しかし，やがて心の空白を自覚するに至り，ついに54年11月23日の夜，〈第2の回心〉と呼ばれる宗教体験を得て信仰に身を捧げることを決意した(その記録として《覚書》がある)。…

※「確率」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」