条件つき確率（読み）じょうけんつきかくりつ

日本大百科全書(ニッポニカ)

条件つき確率
じょうけんつきかくりつ

n本のくじのうち当たりくじがr本ある。初めにAが、続いてBがこのくじを引くとする。Aが当たる確率はr/nである。Aが当たったときBの当たる確率は(r－1)/(n－1)であり、Aが外れたときBの当たる確率はr/(n－1)である。一般に、二つの事象E、Fに対して、Eがおこったという条件のもとにFがおこる確率をp_E(F)と表し、条件つき確率という。前記のくじの例で、Aが当たるという事象をE、Bが当たるという事象をFで表せば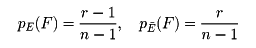

である。ただしĒはEがおこらないこと、すなわちAが外れるという事象を表す。

　次に乗法定理を説明する。二つの事象E、Fに対して、E、Fが両方ともおこる場合の数をa、EがおこりFがおこらない場合の数をb、EがおこらないでFがおこる場合の数をc、E、Fが両方ともおこらない場合の数をdとする。そして総数N＝a＋b＋c＋d個の場合の一つ一つがおこる確率はすべて同じであるとする。このとき、E、Fが両方ともおこる確率をp＝p(E∩F)と表せばp＝a/Nである。次にEのおこる確率p(E)は(a＋b)/Nであり、EがおこったときにFがおこる確率p_E(F)はa/(a＋b)である。したがって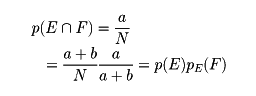

すなわち、E、Fが両方ともおこる確率は、Eがおこる確率p(E)と、EがおこったときFがおこる確率p_E(F)との積に等しい。この関係を乗法定理という。これは二つの事象に関するものであるが、m個の事象についての次の定理も乗法定理という。「m個の事象E₁、E₂、……、E_mがあるとき、E₁のおこる確率をp₁、E₁がおこったときにE₂のおこる確率をp₂、E₁、E₂が両方ともおこったときE₃のおこる確率をp₃、以下同様にp₄……を定めると、E₁、……、E_mがすべておこる確率p(E₁∩……∩E_m)はp₁p₂……p_mに等しい」。とくにE₁、……、E_mが独立であれば
　　p(E₁∩……∩E_m)＝p(E₁)p(E₂)……p(E_m)
である。

　初めにあげたくじの例で、Aが当たるという事象をE、Bが当たるという事象をFで表せば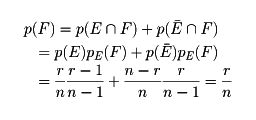

したがって、くじを引くときは1回目に引く人が当たる確率と2回目に引く人が当たる確率は等しい。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

条件つき確率
じょうけんつきかくりつ
conditional probability

条件 B のもとでの A の起る確率をいう。 A や B を外延的に集合で表現しておけば

P(A｜B)＝P(A∩B)｜P(B)

となる。これによって

P(A∩B)＝P(B)P(A｜B)

つまり，A かつ B である確率は，B である確率に，B のときに A の起る確率を掛けたものになる。

出典　ブリタニカ国際大百科事典 小項目事典