確率変数（読み）カクリツヘンスウ

デジタル大辞泉

かくりつ‐へんすう【確率変数】

試行ごとにある確率をもって定まる量。二つのさいころを振る試行で出た目の和のような量。

出典　小学館

精選版 日本国語大辞典

かくりつ‐へんすう【確率変数】

1. 〘 名詞 〙 確率論で、試行の結果に応じて値の定まる変数のこと。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

確率変数
かくりつへんすう

いろいろの値をとりうる変数Xがあって、それぞれの値をとる確率が決まっているときXを確率変数という。たとえば、さいころを投げたとき出る目の数をXと置けば、Xは1から6までの整数のどれかであり、どの値をとる確率も1/6であるからXは確率変数である。また宝くじを買ったとき、当せん金額をXとするとXは確率変数である。はずれた場合はXは0であり、当せんした場合は等級によってXの値は決まり、しかも、各場合の確率は決まっているからである。

　確率変数Xのとりうる値がx₁、x₂、……であって、Xがx_iである確率をp_iとすればp₁+p₂+……=1である。このような確率変数を離散型という。これに対して、ある区間I（無限区間でもよい）のどの値もとりうるような確率変数を連続型という。詳しくいえば、区間Iで連続な関数f(x)が

を満たし、Iに含まれる任意の区間Jに対して、Xの値がJに属する確率が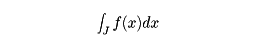

で与えられるとき、Xを連続型の確率変数というのである。測度論的確率論では離散型および連続型を含む一般的な形で確率変数が定義される。この場合、確率変数Xは変数というよりむしろ関数というべきものである。すなわち、確率測度が与えられている標本空間で定義された可測関数のことを確率変数というのである。

［古屋　茂］

[参照項目] | 確率

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

確率変数 (かくりつへんすう)
random variable

偶然現象を記述する場合，重要な手段は数値的情報を用いることである。ところで偶然現象自体は確率空間（Ω，B，P）で表される。Ωは根元事象と呼ばれる偶然を支配するパラメーターωの集合，BはΩ自身も含めΩの部分集合からなる完全加法族，そしてPはBを定義域とするP（Ω）＝1なる測度である。Ω上の関数X（ω）がB-可測のとき確率変数という。これが数値情報を伝えるものである。このXは多次元空間R^dの値をとってもよい。R^dのボレル集合Bに対し，P（X⁻¹（B））＝m（B）とおけばmはR^d上の確率測度になる。これをXの分布という。二つの確率変数X，Yは，もしP（X⁻¹（B）∩Y⁻¹（C））＝P（X⁻¹（B））・P（Y⁻¹（C））が任意のB，Cについて成り立つとき独立であるという。三つ以上の確率変数についても同様に独立の概念が定義される。独立な確率変数列の和は，極限定理など興味ある確率論の話題が多い。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

確率変数
かくりつへんすう
random variable

ある事象の起りうる確率を決定する場合，それには偶然が働いている。確率論では，このような偶然量の性格を明確に定義するが，この偶然量を確率変数という。一般に，ある起りうる事象を数値によって示すのは，この確率変数を考えていることと同じである。それゆえ，標本空間において定義された関数を，確率変数ということができる。いま，標本空間 S における n 個の事象を A₁ ，A₂ ，…，A_n とすると，そのおのおのについて，ある A_i が起ったときに，x_i という値をとるような偶然量 X が確率変数である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の確率変数の言及

【確率】より

…よって，とにかくk回成功する確率は組合せを用いて_nC_kp^kq^n－kであることがわかる。
［確率変数と確率分布］
　n回のベルヌーイ試行で成功する回数をXと書けば，それは偶然によっていろいろな数値をとる変数である。このような変数を確率変数という。…

【統計量】より

…ある一定の確率法則に従っていろいろな値をとる変数を確率変数という。たとえば，母集団から無作為にとったn個の標本x₁，……，x_nは母集団分布に従うn個の確率変数である。…

※「確率変数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」