Β関数（読み）ベータかんすう（その他表記）beta function

改訂新版　世界大百科事典

Β関数 (ベータかんすう)
beta function

x＞0，y＞0なるとき，定積分，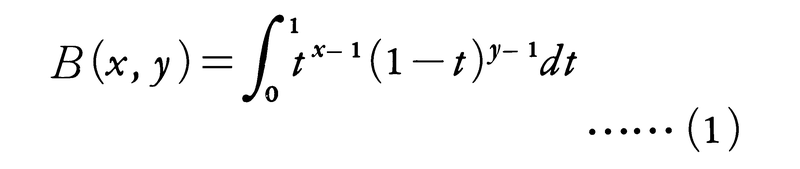

は収束し，xとyの関数となる。これをΒ関数という。これとΓ関数，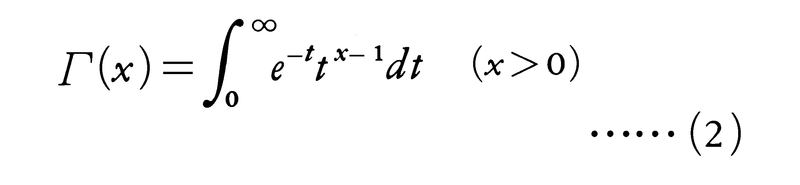

との間には，

なる関係がある。nが正の整数ならば，Γ（n）＝（n－1）！となることは，（2）の右辺で部分積分をn回行って示される。このことと（3）により，正の整数m，nに対して，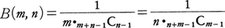

が成立する。ここで_nC_kは二項係数である。x，yが複素数であってもRex＞0，Rey＞0（Rexはxの実数部分）ならば，（1）式の右辺の積分が収束して，Β（x，y）が定義される。さらに，複素変数xのΓ関数Γ（x）と（3）によって，xとyが複素平面上で0または負の整数でない限りΒ（x，y）が定義されることがわかる。（1）の積分の上端1を0＜α＜1なるαで置き換えて定義される関数，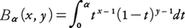

を不完全Β関数という。なお，（1），（2）の積分表示をそれぞれ第1種オイラー積分，第2種オイラー積分という。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のΒ関数の言及

【Γ関数】より

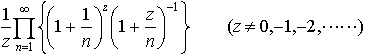…解析学で重要な特殊関数。1929年，L.オイラーは定積分に関連して，次の無限乗積を複素数zに対し導入した。これをA.M.ルジャンドルが，ガンマ関数と命名し，記号Γ(z)を用いた。上の式は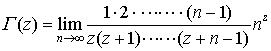，と一致するが，さらに書き直せば，次のワイヤーシュトラスの標準形に変形できる。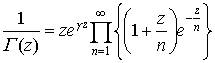ここに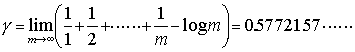，は，オイラーの定数である。ワイヤーシュトラスの標準形からわかるように，Γ関数はz＝0，－1，－2，……で1位の極をもち，その他では解析的になる。…

※「Β関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」