関連語
精選版 日本国語大辞典 「定積分」の意味・読み・例文・類語
てい‐せきぶん【定積分】
ブリタニカ国際大百科事典 小項目事典 「定積分」の意味・わかりやすい解説
定積分
ていせきぶん
definite integral
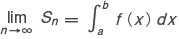 と書いて,f(x) の [a,b] における定積分またはリーマン積分という。つまり,Δx が無限小 dx になったときの和 Σf(x)Δx である。この場合,右辺の記号を積分記号 (これは sum のSの長字体) ,f(x) を被積分関数,a を積分の下端,b を積分の上端という。また右辺の解を求めることを f(x) を a から b まで積分するという。 f(x) が [a,b] で連続であれば,xi および ξi の選び方には無関係に,その定積分は存在する (積分の存在定理) 。定積分には次のような基本的性質がある。
と書いて,f(x) の [a,b] における定積分またはリーマン積分という。つまり,Δx が無限小 dx になったときの和 Σf(x)Δx である。この場合,右辺の記号を積分記号 (これは sum のSの長字体) ,f(x) を被積分関数,a を積分の下端,b を積分の上端という。また右辺の解を求めることを f(x) を a から b まで積分するという。 f(x) が [a,b] で連続であれば,xi および ξi の選び方には無関係に,その定積分は存在する (積分の存在定理) 。定積分には次のような基本的性質がある。 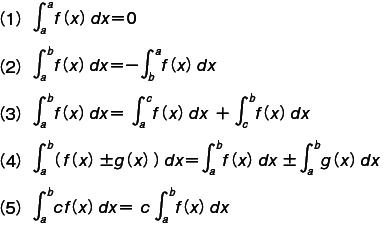 a,b,c は任意の定数である。
a,b,c は任意の定数である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「定積分」の意味・わかりやすい解説
定積分 (ていせきぶん)
→積分
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「定積分」の意味・わかりやすい解説
定積分【ていせきぶん】
出典 株式会社平凡社百科事典マイペディアについて 情報
日本大百科全書(ニッポニカ) 「定積分」の意味・わかりやすい解説
定積分
ていせきぶん
→積分法
世界大百科事典(旧版)内の定積分の言及
【積分】より
…以下,本項ではまず面積を求める方法としての積分の定義を与え,微分演算との関係を述べ,積分の性質や計算法およびその関連事項などを述べる。
[定積分と不定積分]
a≦x≦bなるxの範囲(これを区間[a,b]という)で与えられた関数f(x)があるとき,この区間を, a=x0<x1<x2<……<xn-1<xn=bなる分点xjでn個の小区間に分け,それぞれの小区間[xj-1,xj](j=1,……,n)の長さxj-xj-1に,その区間内の任意の点ξjにおける関数値f(ξj)を掛けて加えた和, f(ξ1)(x1-x0)+f(ξ2)(x2-x1) +……+f(ξn)(xn-xn-1) ……(1) を考える。どの小区間の長さも限りなく小さくなるように分点の数を限りなく増していくとき,この和が,分点やξjのとり方に無関係な一定の値Sに限りなく近づくならば,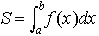 と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。…
と書いて,この値をf(x)のaからbまでの定積分,または単に積分といい,このときf(x)は区間[a,b]において積分可能であるという。…
※「定積分」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


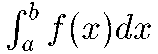 と表わす。負の値をもとる場合には、右の図形のx軸よりも下の部分の面積を負として計算する。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
と表わす。負の値をもとる場合には、右の図形のx軸よりも下の部分の面積を負として計算する。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕