フリン図（読み）フリンず

最新 地学事典

フリンず
フリン図

Flinn diagram

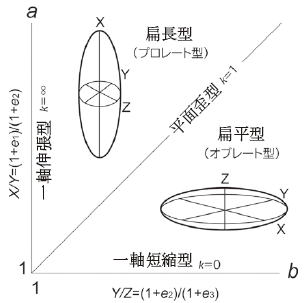
D.Flinn（1962）により導入された歪み楕円体の軸の長さや形を二次元的に表現する図。Flinnは変形プロット（deformation plot）と呼んだ。フリン図では，歪みの主軸をX，Y，Z（X≧Y≧Z）としたとき，縦軸にa=X/Y，横軸にb=Y/Zをとり，任意の歪み楕円体は図上の１点で表される。主歪みをe₁，e₂，e_３（e_１>e_２>e_３）とすると，X＝１＋e₁，Y=１+e₂，Z=１+e_３である。原点を（1，１）とし球の形を表す。楕円体を表す点と原点を結んだ線の傾斜k（=（a−１）/（b−１））は，フリンのk値（Flinn’s k-value）といわれ，楕円体の形状を区分する。体積一定の変形では，歪み楕円体の形状は，k=０のとき，一軸短縮型（uniaxial shorteningまたはuniaxial oblate type），0＜k＜１のとき，扁平型（flattening type），k=１のとき，平面歪み型（plane-strain type），1＜k＜∞のとき，扁長型（constriction type），k=∞のとき，一軸伸張型（uniaxial extensionまたはuniaxial prolate type）になる。フリン図の横軸と縦軸をそれぞれlog bとlog aで置き換えたものを，対数フリン図（logarithmic Flinn diagram）または対数歪み図（logarithmic strain diagram）という。このとき，対数は自然対数でも常用対数でもよい。

執筆者：越谷 信・高木 秀雄

出典　平凡社「最新 地学事典」