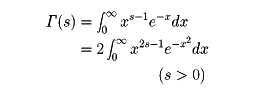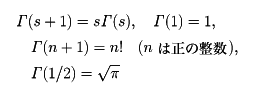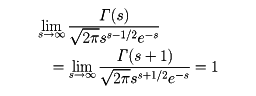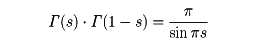ガンマ関数（読み）がんまかんすう

日本大百科全書(ニッポニカ)

ガンマ関数
がんまかんすう

オイラーによって考えられた、階乗を一般化する関数。

で定義される。この関数は

を満たす。sが大きいときのΓ(s)の値を近似的に計算する式に、次のスターリングの公式がある。

　Γ(s)を定義する積分はsが複素数のときも、sの実数部分が正ならば収束し、この関数は、s＝0,－1,－2,……を除いて、複素平面全体に解析接続される。1/Γ(s)は複素平面全体で正則である。また、次の関数等式

は重要である。

［竹之内脩］

[参照項目] | ベータ関数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ガンマ関数
ガンマかんすう
gamma function

第2種オイラー積分ともいう。 α＞0 で定義された関数
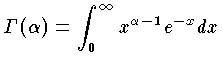をガンマ関数という。ガンマ関数は，次の性質をもつ。
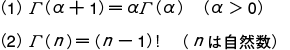この (2) の性質からガンマ関数は，階乗を拡張した関数ということができる。この関数は，オイラーによって発見されたもので，ベータ関数と並んでオイラー積分の名が与えられている。

出典　ブリタニカ国際大百科事典 小項目事典