階乗（読み）カイジョウ（英語表記）factorial

デジタル大辞泉

かい‐じょう【階乗】

1からnまでの連続するn個の自然数の積をnの階乗という。n!と書き、例えば4!＝1×2×3×4＝24と表す。ただし、0の階乗は1とする。

出典　小学館

精選版 日本国語大辞典

かい‐じょう【階乗】

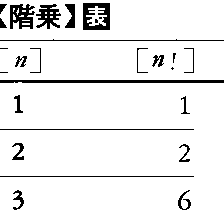
1. 〘 名詞 〙 数学で、ｎが自然数であるとき、１からｎまでのすべての自然数の積のｎに対する称。n! で表わす。たとえば、５の階乗は 5!=5×4×3×2×l=l20 など。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

階乗 (かいじょう)
factorial

自然数nについて，n以下のすべての自然数の積をnの階乗といい，n！で表す。すなわち，n！＝1×2×……×（n－1）×n例えば，n個の異なるものの並べ方の数はn！であり，n個の異なるものから，r個をとり出す組合せの数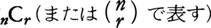は，n・（n－1）……（n－r＋1）/r！に等しい。いま，0の階乗を0！＝1，また，_nC₀＝1と定めれば，_nC_rは0≦r≦nについて，_nC_r＝n ! /r ! （n－r） ! と書くことができ，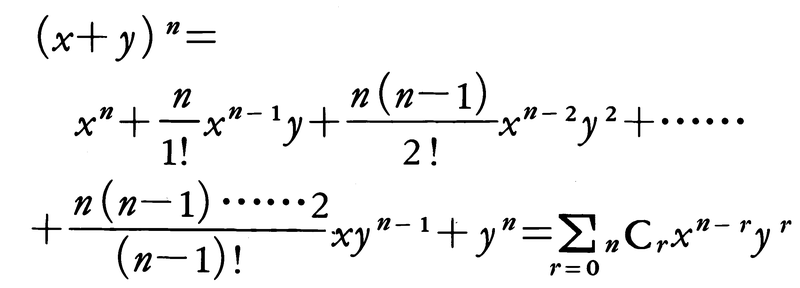

と表される（二項定理）。このことから，_nC_rを二項係数とも呼ぶ。

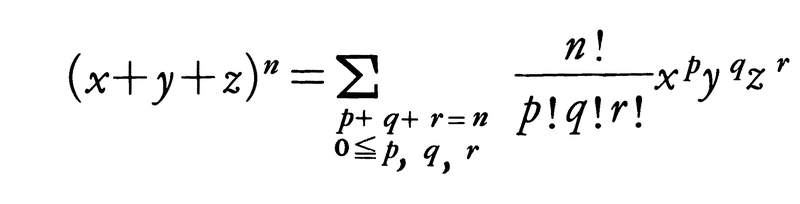
など，多項定理にも階乗の記号が現れ，この場合も，0！＝1とした約束が役に立っている。そのほか，テーラー展開，マクローリン展開など，階乗の記号は，数学の多くの公式中にしばしば現れる。n！は，nが大きくなるとき急速に大きくなるが，もちろんnⁿより小さく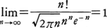，であることが知られている（スターリングの公式）。ここで，πは円周率，eは自然対数の底である。なお，ガンマ関数Γ（x）を用いると，n！＝Γ（n＋1）とも書ける。
執筆者：西村 純一

表

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

階乗
かいじょう

自然数nに対して
n・(n-1)・(n-2)・……・2・1
をnの階乗（ファクトリアルfactorial）といい、n!または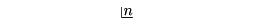

と書く。この値は、n個の異なるものを一列に並べてつくる順列の総数に等しい。また、n個の異なるものからr個とってつくる順列の総数はn!/(n-r)!となるが、この式がn=rのときも形式的に成り立つように0!=1と定義する。

　n!の値は、nが増加するにつれて急激に増加する。たとえば
3!=6, 5!=120, 10!=3628800, 12!=479001600
であり、100!は158桁(けた)、200!は375桁の自然数になる。n!については次の式が成り立つ。

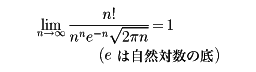
これをスターリングstirlingの公式といい、このことを利用して、nの大きな値に対するn!の近似値を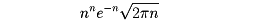

によって計算することができる。

［植竹恒男］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

階乗【かいじょう】

n以下のすべての自然数の積をnの階乗といい，n！と書く。つまりn！＝１×２×３×…×（n−１）×n。０！＝１と定義する。→スターリングの公式
→関連項目e｜順列

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

階乗
かいじょう
factorial

1から始る n個の整数全部の積を，nの階乗といい，これを記号 n!で表わす。すなわち n!＝1×2×3×…×nである。また0!＝1と定義する。

出典　ブリタニカ国際大百科事典 小項目事典