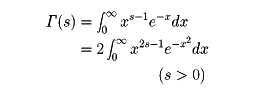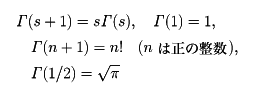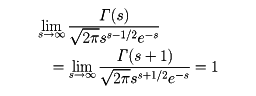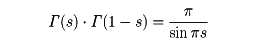ブリタニカ国際大百科事典 小項目事典 「ガンマ関数」の意味・わかりやすい解説
ガンマ関数
ガンマかんすう
gamma function
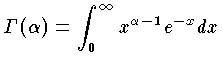 をガンマ関数という。ガンマ関数は,次の性質をもつ。
をガンマ関数という。ガンマ関数は,次の性質をもつ。 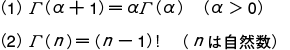 この (2) の性質からガンマ関数は,階乗を拡張した関数ということができる。この関数は,オイラーによって発見されたもので,ベータ関数と並んでオイラー積分の名が与えられている。
この (2) の性質からガンマ関数は,階乗を拡張した関数ということができる。この関数は,オイラーによって発見されたもので,ベータ関数と並んでオイラー積分の名が与えられている。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
二十四節気の一つ。元来,太陰太陽暦の 12月中 (12月後半) のことで,太陽の黄経が 300°に達した日 (太陽暦の1月 20日か 21日) から立春 (2月4日か5日) の前日までの約 15日間で...
1/16 デジタル大辞泉プラスを更新
1/16 デジタル大辞泉を更新
12/10 小学館の図鑑NEO[新版]魚を追加
10/17 ブリタニカ国際大百科事典 小項目事典を更新
8/22 日本大百科全書(ニッポニカ)を更新