精選版 日本国語大辞典 「ピタゴラスの定理」の意味・読み・例文・類語
ブリタニカ国際大百科事典 小項目事典 「ピタゴラスの定理」の意味・わかりやすい解説
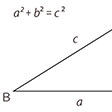
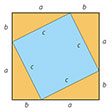
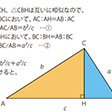
ピタゴラスの定理
ピタゴラスのていり
Pythagorean theorem
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「ピタゴラスの定理」の意味・わかりやすい解説
ピタゴラスの定理【ピタゴラスのていり】
出典 株式会社平凡社百科事典マイペディアについて 情報
改訂新版 世界大百科事典 「ピタゴラスの定理」の意味・わかりやすい解説
ピタゴラスの定理 (ピタゴラスのていり)
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「ピタゴラスの定理」の意味・わかりやすい解説
ピタゴラスの定理
ぴたごらすのていり
法則の辞典 「ピタゴラスの定理」の解説
ピタゴラスの定理【Pythagorean theorem】
世界大百科事典(旧版)内のピタゴラスの定理の言及
【三平方の定理】より
…これはユークリッド幾何学におけるもっとも重要な定理の一つで,三平方の定理と呼ばれている。この定理は古代ギリシアの哲学者ピタゴラスによって発見されたといわれ,ピタゴラスの定理とも呼ばれているが真偽のほどは定かでない。三平方の定理の逆も成り立つ。…
※「ピタゴラスの定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...