日本大百科全書(ニッポニカ) 「ラプラス展開」の意味・わかりやすい解説
ラプラス展開
らぷらすてんかい
Laplace's expansion
行列式を、より小さい行列式の計算で求める方法にラプラス展開がある。
A=(aij)をn次正方行列とする。1≦i1<i2<……ir≦nと1≦j1<j2<……jr≦nに対し、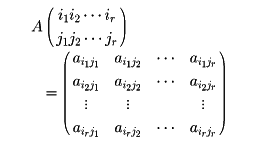
のようにr次の正方行列をつくる。これはAのn個の行のうちの第i1、第i2…第ir行上と、n個の列のうちの第j1、第j2…第jr列との上にあるaijをそのままの順序で取り出してつくったr次の正方行列である。このような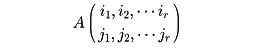
をAのr次の小行列といい、その行列式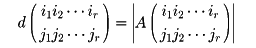
をAのr次の小行列式という。たとえば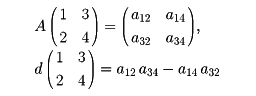
いま、1、2…nから1≦i1<i2<…ir<nを取り去った残りをi′1<i′2<…<i′n-rとし、j1<j2<…<jrに対しても、同様のものをj′1<j′2<…<j′n-rとすると、Aの行列式|A|は次の式で与えられる。
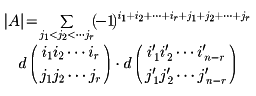
ただし、ここで右辺の和は、i1<i2<…<irを固定し(したがってi′1…i′n-rも固定され)、1≦j1<j2<…<jr≦nのようなあらゆる組についての総和である。この式をAの行列式の第i1、第i2…第ir行によるラプラス展開という。
以上の式でj1<j2<…<jrを固定し、Σを1≦i1<i2<…<ir≦nのようなあらゆる組についての和にした式も成り立ち、第j1、第j2…第jr列によるラプラス展開という。たとえば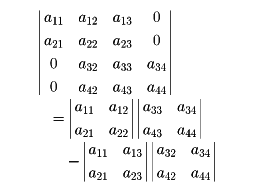
r=1のラプラス展開は、それぞれ第i1行、第j1列による行列式の展開式である。
[菅野恒雄]

