可測集合（読み）かそくしゅうごう（英語表記）measurable set

改訂新版　世界大百科事典

可測集合 (かそくしゅうごう)
measurable set

Rをユークリッド空間とする。Rにおける面積や体積の概念の拡張であるルベーグ測度が定義されている集合をルベーグ可測集合という。ルベーグ可測集合の全体をMと書くことにするとMは次の性質をもつ。

（1）空集合φはMに属する。

（2）A∈Mならば，その余集合R－A∈M。

（3）A₁，A₂，……，A_n，……∈Mならばそれ

　らの合併集合A＝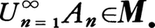

この三つの性質から次のようなことが導かれる。

（4）全空間RはMに属する。

（5）Mに属する集合の合併，差，共通部分を作る演算をたかだか可算無限回行って得られる集合はMに属する。一般の空間Rの部分集合の族Mが上の（1）（2）（3）をみたすならば，Mを定義域とする測度を定義することができる。このようなMが与えられたとき，これに属する集合を可測集合ということがある。現代の測度論は，このような一般の空間で構成される。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」