測度（読み）ソクド

デジタル大辞泉

そく‐ど【測度】

［名］(スル)
１ はかること。特に、度数などをはかること。
「この星の軌道及び動転の遅速を精くわしく―して」〈中村訳・西国立志編〉
２ 数学で、長さ・面積・体積の概念の拡張として、一般の集合の部分集合に対して定義される量。

出典　小学館

精選版 日本国語大辞典

そく‐ど【測度】

1. 〘 名詞 〙
2. ① 度数・尺度などをはかること。計測。測定。
   1. [初出の実例]「この星の軌道、及び動転の遅速を精く測度して」(出典：西国立志編（1870‐71）〈中村正直訳〉五)
3. ② 各種の量をはかる単位。尺度。また、ある単位で、ある量をはかったときに得られる数値。
   1. [初出の実例]「日月五星の測度も、唐日本とは、余ほどかわれり」(出典：紅毛談（1765）上)
4. ③ 数学で、長さ・面積・体積の概念の拡張として、一般の集合の部分集合に対して定義される量。ジョルダン測度、ルベーグ測度などがある。
5. ④ ⇒そくたく（測度）

そく‐たく【測度】

1. 〘 名詞 〙 あれこれとおしはかること。忖度(そんたく)。推量。
   1. [初出の実例]「世尊向の所説の如くんば、甚だ思議し難し、亦測度し難し」(出典：三国伝記（1407‐46頃か）八)
   2. [その他の文献]〔礼記‐礼運〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

測度
そくど

直線上の区間I=［a,b］の長さはb-aであるが、これを|I|で表す。直線上の集合Eにつねに長さに相当するような量m(E)を定義できないかという問題がある。そのとき量m(E)（Eの測度という）は理想的には次の性質をもつことが望ましい。

（1）m(E)≧0はすべての集合Eに定義され、
（2）Eが区間Iのときは
　　　m(I)=|I|
（3）｛E_n｝が互いに共通部分をもたないとき、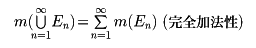

（4）集合Eをaだけ平行移動することをa+Eで表すと、
　　m(a+E)=m(E)
　しかし、このような測度を、すべての集合に定義することはできないことがわかっている。ルベーグは、Eをまず可算個の区間の列｛I_n｝で覆い（つまり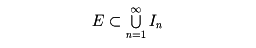

とする）、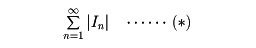

を考える。Eのいろいろな覆い方のうち、（＊）の最小値をm^*(E)で表し、Eの外測度という。外測度は任意の集合Eに対して定義されており、
　　m^*(E)≧0,　m^*(∅)=0
　　　(∅は空集合)
　　E⊂Fならばm^*(E)≦m^*(F)
など、大きさを測る量としての基本的な性質をもっているが、集合E、Fが共通部分をもたないときでも、
　　m^*(E∪F)=m^*(E)+m^*(F)
　　　（加法性）
とは限らない。そこで、任意の集合Aに対し、
　　m^*(A)=m^*(A∩E)+m^*(A∩Ē)
が成立する集合Eを可測集合といい（ĒはEの補集合）、
m(E)=m^*(E)をEの測度と定義する。すると、m^*(E)=0ならばEは可測集合、また、開集合や閉集合などの基本的な集合はすべて可測集合になる。このように、測度を可測集合の族Mだけで考えることにすると、測度は前述の（1）～（4）の性質をもつ。

　測度の概念は次のように抽象化することができる。任意の集合Xをとり、その部分集合のある族Mを考える。Mの要素E∈Mに、負にならない数m(E)が定義されて、これが前に述べた（1）～（3）を満足するとき、E∈Mを可測集合、m(E)をEの測度といい、これらをひとまとめにして｛X,M,m｝を測度空間という。測度空間が与えられると、そこで定義された関数にルベーグ積分を定義することができるが、ルベーグ積分のよさは、測度空間の完全加法性による。測度空間で、とくに全空間Xが測度1をもつとき、確率空間といい、確率論はここで展開される。最後に、集合Xが位相群のとき、a,b∈Xの積をabと書くとき、前述の（1）から（3）までと、（4）のかわりに、
（4）′m(a^-1E)=m(E)
を要求した測度をハールの測度といい、位相群のうえで解析学をするのに重要な役割をする。

［洲之内治男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

測度
そくど
measure

1次元における長さ，2次元における面積，3次元における体積などの概念を，一般の集合にまで無理のないように拡張して一般化，抽象化した概念である。 E.ボレルや H.ルベーグが，C.ジョルダンの集合に関する容積 extent (→ジョルダン測度 ) の定義を改良してさらに一般化し，今日の測度の概念を得た。 m 次元ユークリッド空間 R^m 内の任意の点集合を A とする。このとき開区間の列 {I_n} をつくると，そのたかだか可算個の I_n(n＝1，2，3，…) の合併集合 ∪I_n で A をおおうことができる。このようなあらゆる区間列の容積の和 Σ_n｜I_n｜ の下限 inf {Σ_n｜I_n｜：A⊂∪I_n}＝m^*A を，A のルベーグ外測度，あるいは単に外測度という。外測度 m^*A には次の性質がある。
以上の4つの条件を満足する m^*A を，逆に外測度の定義とすることもできる。この場合，m^*A をカラテオドリー Caratheodory の外測度という。 A のほかに R^m の任意の集合 X をとると，条件(4) から m^*A≦m^*(X∩A)＋m^*(X∩A^c) が成り立つが，特に m^*A＝m^*(X∩A)＋m^*(X∩A) であれば，R^m の点集合 A は可測であるという。このときの m^*A を mA あるいは ｜A｜ と書き，A のルベーグ測度，あるいは単に測度という。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

測度 (そくど)
measure

平面上の簡単な図形は面積が定義される。一般に，平面上の点集合Aが面積をもつときに，その面積を｜A｜と書くことにする。集合A₁，A₂，……，A_nがいずれも面積をもち，どの二つも互いに交わらないならば，それらを合併した集合A＝A₁∪A₂∪……∪A_nも面積をもち｜A｜＝｜A₁｜＋｜A₂｜＋……＋｜A_n｜となる。しかし，集合の無限列A₁，A₂，……，A_n，……については，このことは成り立たない。直線上の図形の長さ，空間図形の体積の概念についても同様なことがいえる。

　20世紀の初めにH.ルベーグは，測度と名付ける次のような概念を導入して，その具体的構成法を与えた。すなわち，集合Aの測度μ（A）とは，長さ，面積，体積の概念の拡張であって，可算無限個の集合A₁，A₂，……，A_n，……が測度をもちどの二つも交わらないならば，それらの合併集合A＝A₁∪A₂∪……∪A_n∪……も測度をもち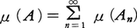となるものである。この性質を完全加法性，または可算加法性という。この測度を現在ではルベーグ測度と呼ぶ。このような測度の概念を用いて定義される積分をルベーグ積分という。ルベーグ積分においては，測度の可算加法性のおかげで，従来の面積や体積を用いて定義された積分（リーマン積分）よりも極限操作などがはるかに容易になり，ルベーグ積分論は20世紀の解析学に目覚ましい発展をもたらした。
→積分論
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

普及版 字通

【測度】そくたく

はかる。〔礼記、礼運〕欲惡は心の大端なり。人は其の心を(かく)し、測度すべからざるなり。美惡皆其の心に在りて、其の色に見(あら)はれず。

字通「測」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の測度の言及

【拍子】より

…西洋近代の5線記譜法では，視覚的便宜をはかって，拍のまとまりごとに縦線が引かれている。これを小節線bar,bar‐lineといい，これによって仕切られた1区画を小節bar,measureという。一つの小節は拍子の1単位に相当し，原則として小節線のすぐ後の拍(第1拍)が強拍(下拍ともいう)にあたる。…

【約数】より

…自然数aが自然数bを割りきるとき，aはbの約数であるという。たとえば，13は52の約数である。aがbの約数であるとき，bはaの倍数である。多項式f,gに対しても，fがgを割りきるとき，fはgの約数であるという。【杉江 徹】…

【確率】より

…すなわち，　P(A)＝P(A₁)＋P(A₂)＋……　こうした性質をもつ組(Ω，B，P)を確率空間と呼び，数学的な議論が展開される場となる。ここでPは解析学で測度といわれているものにほかならないが，P(Ω)＝1となる特別な測度である。　例2　二つのさいを投げたとき，目の出方は6×6＝36通りある。…

※「測度」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」