同形写像 どうけいしゃぞうisomorphic mapping

ブリタニカ国際大百科事典 小項目事典

同形写像
どうけいしゃぞう
isomorphic mapping

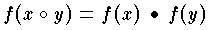二つの代数系 R，R'があり，R では結合演算∘が，R'では結合演算 ∙ が定義されているものとする。このとき写像 f：R→R'が全射であって，任意の x，y∈R について，条件 が満たされているとき，写像 f を準同形写像といい，特にこの f が全単射であるとき，f を同形写像という。f が同形写像であれば，R と R'は同形 isomorphismであるといい R≅R'で表す。たとえば，整数全体がつくる加群を Z，偶数全体がつくる加群を E とすれば，関数 f（x）＝2x は，Z から E の上への一対一写像，すなわち全単射となるから，この関数は同形写像である。代数構造以外の構造についても，その構造を保存する全単射のことを同形写像ということもある。構造によって，順序同形とか位相同形といった使い方もある。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

同形写像
どうけいしゃぞう

→ 準同形写像

出典　小学館　日本大百科全書(ニッポニカ)