加群（読み）カグン（その他表記）module

デジタル大辞泉

か‐ぐん【加群】

可換群のうち、算法が加法であるもの。

出典　小学館

改訂新版　世界大百科事典

加群 (かぐん)
module

平面のベクトルの全体Vを考えると，加法に関して可換群をなしていて，零ベクトル0が加法に関する群としての零（群としての単位元）である。さらに，aがベクトル，rが実数であれば，r・aがベクトルになっていて，次の条件を満たしている。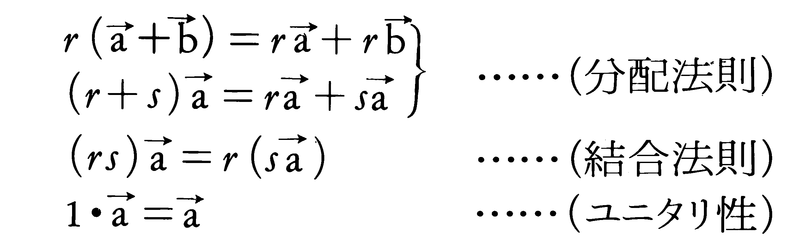

もっと一般にMが加法に関して可換群を作っていて，Rが環であって，Rの元rとMの元mとの間の乗法が，その積rmがMの元であるように定まっていて，さらに上と同様の条件（分配法則，結合法則，ユニタリ性）が満たされているとき，MはR左加群（Rの元が左からかけられるから）という。ただし，ユニタリ性を除外して加群を定義し，ユニタリ性を満たすものをユニタリ加群と定義する立場もある。R左加群Mの部分集合Nが部分加群であるというのは，単に加法に関して部分群ということだけでなく，r∈R，m∈Nならば，rm∈Nの成り立っているときにいう。この場合，NがR左加群となっている。このとき，群としての剰余類群M/Nが考えられるが，r∈R，m＝（m＋N）∈M/Nに対して，rm＝（rm＋N）（すなわち，剰余類mの代表元mを任意にとり，rmの含まれる剰余類がrm）と定めることによって，M/NにR左加群の構造を考える。すると群のときと同様に，次のことがいえる。

　M，M′がR左加群であるとき，MからM′への準同型φとはMからM′への写像で，

　φ（m＋m′）＝φ（m）＋φ（m′）

　φ（rm）＝r（φ（m））

が，任意のm，m′∈M，r∈Rについて成り立つときにいう。NがMの部分加群であれば，Mの元mに対して，mを含む剰余類m＝（m＋N）を対応させる写像は準同型であり，逆に，上のような準同型φがあれば，φの核φ⁻¹（0）＝｛m∈M｜φ（m）＝0｝はMの部分加群で，φ（M）はM′の部分加群になり，そのR左加群としての構造はM/φ⁻¹（0）と同じ（すなわち同型）。

　Rの元とMの元との乗法が，Rの元を右からかける形できまっているとき，R右加群が同様の条件（m，n∈M，r，s∈R⇒（m＋n）r＝mr＋nr，m（r＋s）＝mr＋ms，m（rs）＝（mr）s，m・1＝m）によって定義される。

　Rが可換環であれば，R左加群Mに対して，右からの乗法をmr＝rmと定めてR右加群とすることができるので，右，左の区別は不要となるので，このときは，たんにR加群という。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

加群
かぐん
module

モジュールともいう。ベクトル空間の理論，すなわち線形代数は，実係数もしくは複素係数のように体を係数として考えるのが普通であるが，整数係数とか多項式係数のように，環を係数として考えなければならないこともある。このとき，加群という。結合を加法で表わしたアーベル群では，n 倍が加法から定まるので，整数環 Z を係数とする加群と考えられる。現在の線形代数は，加群の理論として展開され，数学のすべての分野の基礎となっている。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の加群の言及

【モデュール】より

…モジュールともいう。測定単位あるいは機能単位を示す用語として多くの技術分野で用いられている。古い用語としてギリシア，ローマの石造建築の比例を定めるために用いられた〈モドゥルス〉があり，ローマ時代にウィトルウィウスによって著された《建築十書》には，円柱基部の直径を1モドゥルス，すなわち寸法の基本単位として，柱の高さや柱間など神殿各部の寸法を導く方法が詳述されている。現代の建築モデュールもやはり寸法の単位であるが，比例のためというよりもむしろ量産構成材のための寸法規格という意味合いが強い。…

【可換群】より

…　0以外の有理数全体，0以外の実数全体，0以外の複素数全体などは，乗法に関して，可換群をなす。加法に関して可換群をなすものを，加群または加法群と呼ぶ。可換群の他の例としては，群Gの一つの元aで生成された群A(これを巡回群という。…

【環】より

…そこで，集合Aに，その2元a,bの和a＋bを対応させる加法および積a･bを対応させる乗法が定義され，それらが次の公理を満たすとき，Aを環と呼ぶ。
［公理］
　(1)加法に関し，加群をなす。　(a)a＋b＝b＋a　(b)(a＋b)＋c＝a＋(b＋c)　(a,b,c∈A)　　(c)a＋x＝bは必ずただ一つ解をもつ。…

※「加群」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」