ブリタニカ国際大百科事典 小項目事典 「擬球面」の意味・わかりやすい解説
擬球面
ぎきゅうめん
pseudosphere
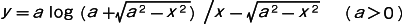を y 軸 (漸近線) のまわりに回転してできる曲面の全曲率は，いたるところ負で一定である。この曲面を擬球面という。擬球面上の測地線を直線，またその上の2点間の距離を変えない変換を運動と考えれば，この曲面上ではロバチェフスキー＝ボーヤイの非ユークリッド幾何学の小域的性質が成り立つ。このことは，イタリアの幾何学者 E.ベルトラミ (1835～1900) によって初めて示された。そのためベルトラミの擬球面とも呼ばれる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報