漸近線（読み）ゼンキンセン（英語表記）asymptote

デジタル大辞泉

ぜんきん‐せん【漸近線】

ある曲線が、原点から無限に遠ざかるにつれて、限りなく近づいてはいくが、決して交わらないし、接しもしない直線。

出典　小学館

精選版 日本国語大辞典

ぜんきん‐せん【漸近線】

1. 〘 名詞 〙 曲線に次第に近づいて行く直線。限りなく遠くまで続く曲線において、動点が曲線に沿って無限に遠ざかるとき、その点からの距離が限りなく０に近づくような定直線が存在すれば、この定直線をその曲線の漸近線という。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

漸近線 (ぜんきんせん)
asymptote

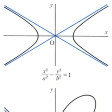
平面上に曲線Cがあって，Cは無限の遠くまで伸びている部分弧C₀をもち，十分遠くのC₀上の各点において接線がひけるものとする。いま，点PをC₀に沿って限りなく遠くへ動かすとき，PにおけるC₀の接線が限りなく近づくような一定の直線が存在するならば，この直線を曲線Cの漸近線という。例えば，y＝1/xのグラフをCとするとき，Cは図のように二つの部分弧C₀とC₀′よりなり，C₀上の点Pにおける接線はPを右のほうに遠ざければ直線y＝0に，上のほうに遠ざければ直線x＝0に限りなく接近し，C₀′上の点における接線については同様のことが“右”“上”を“左”“下”におきかえていえる。したがって2直線x＝0，y＝0はy＝1/xのグラフの漸近線となる。
執筆者：中岡 稔

図－漸近線

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

漸近線
ぜんきんせん
asymptote

曲線 C が無限遠の近くで直線 L に近づくとき，L を C の漸近線という。たとえば，C が y＝f(x) で表わせるとき，x→a のとき f(x)→∞ ならば，直線 x＝a は C の漸近線になる。 x→＋∞ については，L を y＝mx＋b とすると f(x)～mx ，f(x)－mx～b ，すなわち
にすればよい。 L が直線でない場合も，漸近曲線という用語で使うことがある。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

漸近線
ぜんきんせん

平面上の曲線F(x,y)=0があり、動点Pが曲線に沿って原点から無限に遠ざかるとき、Pからの距離が無限小となる定直線が存在する場合、この直線をこの曲線の漸近線という。漸近線をもつ曲線の例としては、双曲線、デカルトの葉形などがある。曲線が直交座標でなく、極座標についてF(r,θ)=0の形で与えられるときも、漸近線は考えられる。コンコイドの場合がそうである。

　漸近線の方程式をy=mx+bとする。曲線に沿って点が無限に遠ざかるとき、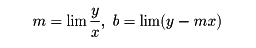

であり、逆にこのような値m、bがあるならば、y=mx+bはこの曲線の漸近線になる。ここでlimは、曲線上の点のx座標、y座標を用いて計算される値を、曲線に沿って点を無限に遠ざけたときの極限値であることを表している。

［竹之内脩］

漸近線

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

漸近線【ぜんきんせん】

曲線Cの一部が無限に延びているとき，C上の点Pにおける接線が，Pが原点から限りなく遠ざかるにつれて一定の直線lに限りなく近づくとき，lをCの漸近線という。たとえば双曲線xy＝１では二つの座標軸（x＝０，y＝０）が漸近線。
→関連項目双曲線

出典　株式会社平凡社