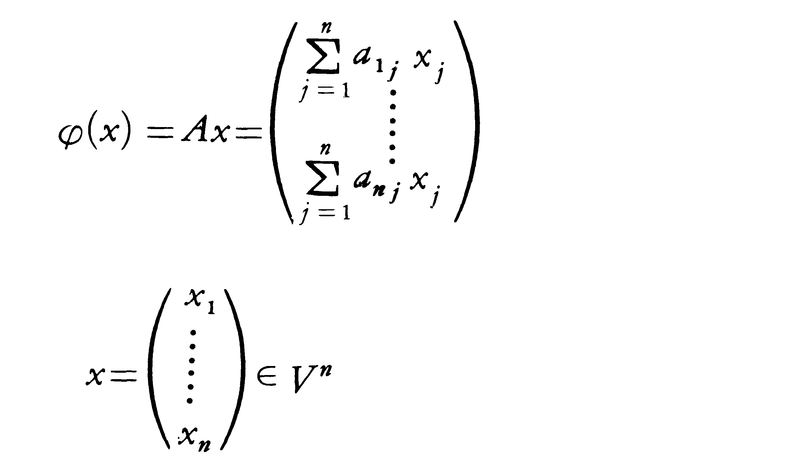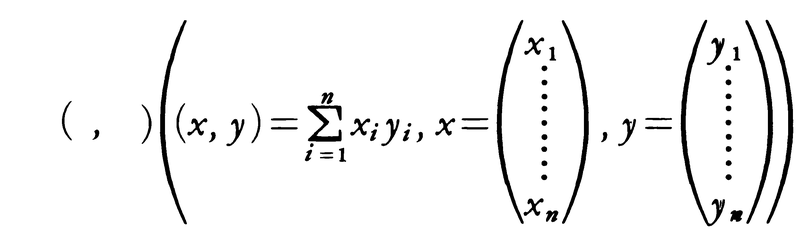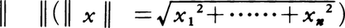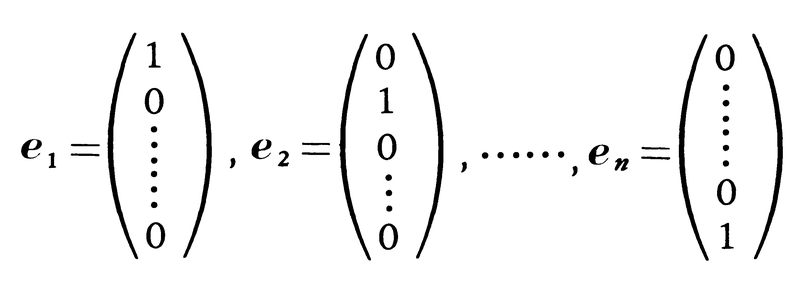直交変換 (ちょっこうへんかん)
orthogonal transformation
実数係数のn次元の縦ベクトル全体をVnで記すことにする。n=2の場合,直交行列は,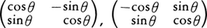 で表されるが,一般にn次の直交行列Aで与えられるVnの一次変換,
で表されるが,一般にn次の直交行列Aで与えられるVnの一次変換,
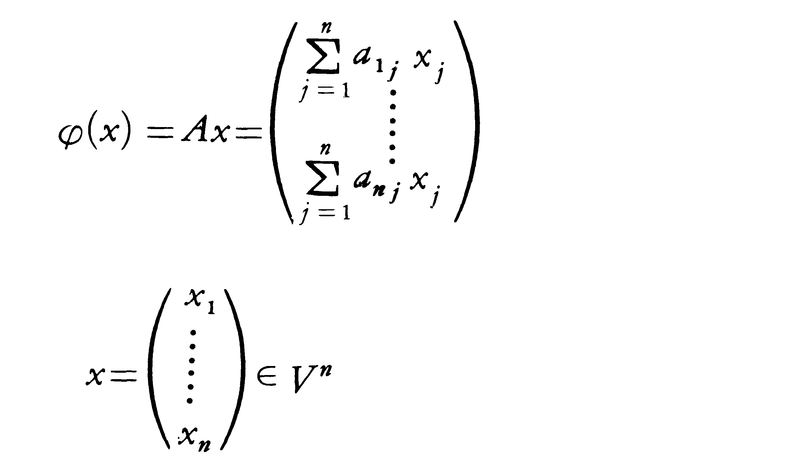
を直交変換という。直交変換はVnの内積
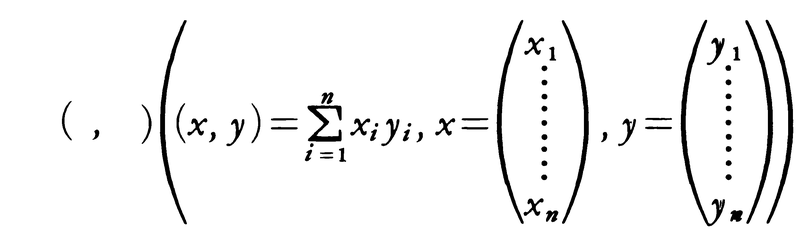
および長さ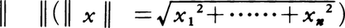
を不変にする。すなわち,(φ(x),φ(y))=(x,y),/φ(x)/=/x/を満たす。逆に内積,または長さを不変にする一次変換は直交変換である。
Vnの基底x1,……,xnが(xi,xj)=δijを満たすとき,この基底を正規直交基底という。例えば,
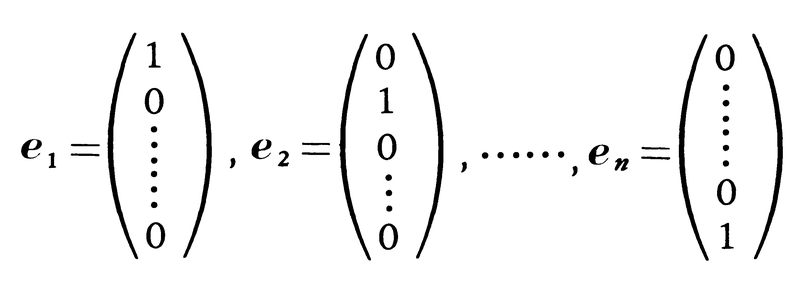
は正規直交基底である。φが直交変換ならば,φ(e1),φ(e2),……,φ(en)は正規直交基底である。逆に,φ(e1),φ(e2),……,φ(en)が正規直交基底ならばφは直交変換である。
ユークリッド空間の合同変換は平行移動とある点での直交変換の合成として表せる。
執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
直交変換
ちょっこうへんかん
orthogonal transformation
1次変換 y=Ax において tAA=E であるとき,この変換を直交変換といい,A を直交行列という。ここに tA は A の転置行列,E は単位行列である。この場合 tA は A の逆行列 A-1 に等しい。以上から直交変換は,直交行列で表わされる1次変換ということができる。直交変換においては,すべてのベクトルの絶対値が不変である。平面上の回転や回転後の折返しという操作は,確かに長さを変えないから,これらは直交変換である。この例からも明らかなように,直交変換は原点を動かさない合同変換である。またすべての合同変換では,直交座標系を直交座標系へ移すから,直交変換は,直交座標系を直交座標系へ移す1次変換であるといってもよい。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
直交変換
ちょっこうへんかん
平面または空間を自分自身に写す写像で、内積(点の座標の成分どうしの積の和)を変えないようなものをいう。基本的なものとして、平面においては、原点の周りの回転移動、x軸に関する対称移動、空間においては、原点を通る直線を軸とする回転移動、xy平面に関する対称移動、がある。平面と空間それぞれにおいて、これらの2種類の移動を組み合わせたものも、あるいはすべての点を動かさない写像も直交変換である。したがって、直交変換は合同変換でもあり、線形変換でもある。二つの直交変換を組み合わせたものもまた直交変換になることから、直交変換の全体は群をなすことがわかる。これを直交(変換)群という。正規直交系が二つ与えられたとき、一方を他方に写すような直交変換が一つだけ定まるが、これは直交変換の基本的性質である。以上では平面と空間について考えたが、もっと一般に、計量ベクトル空間の内積を変えない変換も直交変換という。
[高木亮一]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
世界大百科事典(旧版)内の直交変換の言及
【座標】より
…一次変換(3)では,行列AはdetA≠0でありさえすればよく,これは一次変換としてもっとも一般の場合である(一次変換群)。Aが直交行列の場合,すなわちAの転置行列tAがAの逆行列に等しい(tAA=AtA=1)場合の一次変換は直交変換,さらにdetA=1の場合は固有回転,detA=-1の場合は非固有回転と呼ばれる。(2)で示した実例は平面上の固有回転である。…
※「直交変換」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
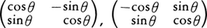 で表されるが,一般にn次の直交行列Aで与えられるVnの一次変換,
で表されるが,一般にn次の直交行列Aで与えられるVnの一次変換,