順序集合（読み）じゅんじょしゅうごう（英語表記）ordered set

改訂新版　世界大百科事典

順序集合 (じゅんじょしゅうごう)
ordered set

実数の大小関係≦は次の性質をもっている。（1）a≦a（反射律），（2）a≦b，b≦cならば，a≦c（推移律），（3）a≦b，b≦aならば，a＝b（反対称律）。これを一般化して，集合Mに関係≦が定まっていて，上記（1）（2）（3）の性質をもつとき，Mは順序集合であるという。一つの集合Sを固定して，Sの部分集合A，Bについて，A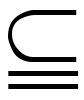Bのとき，A≦Bと決めれば，Sの部分集合全体の集合Tは順序集合になる。しかし，例えばδの相異なる二元s，tを取って，A＝｛s｝，B＝｛t｝とすれば，A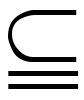BでもB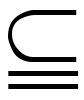Aでもない。すなわち，A，B∈Tについて，A≦B，B≦Aのどちらも成立しないことがある。実数の大小関係のように，かってな二元a，bを取ってきたとき，a≦bかb≦aのどちらかが成立する順序集合を全順序集合と呼ぶ。順序集合Mの部分集合Nについて，a∈MがNの上界であるとは，すべてのb∈Nについて，b≦aが成立することである。部分集合Nに上界があるとき，Nは上に有界であるという。Nの上界全体の集合N′に最小元c（すべてのa∈N′について，c≦a）があれば，それをNの上限と呼ぶ。上のb≦aをa≦bと置きかえて，同様に下界，下に有界，下限が定義される。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

順序集合
じゅんじょしゅうごう

「順序」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典