翻訳|bounded
精選版 日本国語大辞典 「有界」の意味・読み・例文・類語
う‐かい【有界・有海】
日本大百科全書(ニッポニカ) 「有界」の意味・わかりやすい解説
有界
ゆうかい
bounded
集合が無限に遠くの要素を含まないことを言い表す術語。次の2通りの用法がある。
順序集合、すなわち要素の間に大小関係≦の定義されている集合Sにおいて、その一つの部分集合Aに対し、Sのある要素sがあって、Aのどの要素aに対してもa≦sとなるとき、Aは上に有界であるという。このときsはAを上から押さえる、あるいはAの一つの上界であるという。
また、Sの部分集合Bに対して、Bを下から押さえるSの要素があるとき、Bは下に有界であるという。
上に有界、かつ下に有界であるような部分集合は、単に有界であるという。
[竹之内脩]
ブリタニカ国際大百科事典 小項目事典 「有界」の意味・わかりやすい解説
有界
ゆうかい
bounded
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の有界の言及
【関数解析学】より
…
【バナッハ空間論】
バナッハ空間Xからバナッハ空間Yの中への作用素Tが, T(αx+βy)=αTx+βTy (x,y∈X;α,βは複素数) を満たすとき,Tを線形作用素という。また正数γが存在して∥Tx∥≦γ∥Tx∥が成り立つときTは有界であるといい,このようなγの下限を∥T∥と書いて,作用素Tのノルムnormという。線形作用素Tが連続,すなわち,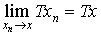 を満たすこととTが有界なこととは同等である。…
を満たすこととTが有界なこととは同等である。…
【上界】より
…aが集合Eの上界であれば,aより大きい数はすべてEの上界である。上界が存在するときEは上に有界boundedであるという。上界が存在しなければ,Eはいくらでも大きい数を含む。…
※「有界」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


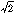 となるような有理数xの集合)。もし、いちばん小さいものがあるときは、それをAの最小上界あるいは
となるような有理数xの集合)。もし、いちばん小さいものがあるときは、それをAの最小上界あるいは