関連語
世界大百科事典(旧版)内のラプラスの展開定理の言及
【小行列式】より
…これは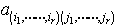 の余因子といわれる。(i1,……,ir),(j1,……,jr)を固定すると,
の余因子といわれる。(i1,……,ir),(j1,……,jr)を固定すると,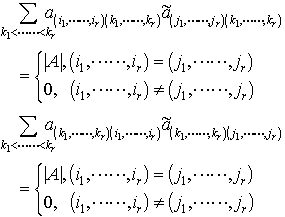 これは行列式のある行または列についての展開の一般化になっており,ラプラスの展開定理といわれる。【丸山 正樹】。…
これは行列式のある行または列についての展開の一般化になっており,ラプラスの展開定理といわれる。【丸山 正樹】。…
※「ラプラスの展開定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

