ガウス過程（読み）ガウスかてい（その他表記）Gaussian process

改訂新版　世界大百科事典

ガウス過程 (ガウスかてい)
Gaussian process

時間を表す変数tと偶然を表す媒介変数wの関数である確率過程X（t，w）（wは省略して単にX（t）と書くことが多い）は，任意に選んだn個の時点t₁，t₂，……，t_nに対して，ベクトル（X（t₁），X（t₂），……，X（t_n））がいつも多次元ガウス分布に従うとき，ガウス過程あるいは正規過程と呼ばれる。X（t）の平均値E（X（t））＝m（t）と共分散関数E｛（X（t）－m（t））（X（s）－m（s））｝＝Γ（t，s）がわかれば，このガウス過程の分布，とくに上記ベクトルの分布は一意的に決まる。時間変数tが離散的な場合は，ガウス型時系列とも呼ばれ詳しい性質が知られている。とくにその分布が時間の推移に関して不変な場合，すなわち定常過程の場合は平均値は定数になり，Γ（t，s）はt－sのみの関数γ（t－s）となる。このγに対して，単調増加関数Fを用いたスペクトル分解，が得られる。dF（λ）はスペクトル測度と呼ばれるが，これと平均値とで与えられた定常ガウス過程の分布が完全に決定される。自然界に現れるガウス型のノイズは，このようなスペクトル測度で特徴づけられることが多い。連続時間のとき基本となるのはブラウン運動（ウィーナー過程ともいう）B（t）であって，その性質はよく知られている。より一般のガウス過程としては，B（t）により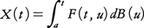，と表現されるものがある。Fはwを含まない関数で，上式は各tに対しX（t）がB（t）の微小増分dB（u）にウェイトF（t，u）を乗じたものの和として得られることを示す。関数Fの性質を通じてX（t）の構造が解明される。とくにX（t）が定常過程なら，a＝－∞として，Fはt－uのみの関数となる。その重要な例としてはF（t－u）＝c exp［－λ（t－u）］，u≦tとなるもの，すなわちオルンシュタイン=ウーレンベックOrnstein-Uhlenbeckのブラウン運動がある。それはいわゆるランジュバン方程式の解になる。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

法則の辞典

ガウス過程【Gaussian process】

m 次元の確率過程 X（t）において，すべての同時確率分布関数

F_nm（x₁，t₁;x₂，t₂;…：x_n，t_n）

＝P ｛X（t₁）≦x₁，X（t₂）≦x₂，…，X（t_n）≦x_n ｝

がガウス分布＊なら，X（t）はガウス過程であるという．

出典　朝倉書店

世界大百科事典（旧版）内のガウス過程の言及

【確率過程】より

…時刻0からtまでの間に起きるある種の交通事故の件数をX_t(ω)とするとき，｛X_t(ω)｝がポアソン過程とみなされる場合がある。　確率過程のうち，ガウス過程，定常過程，加法過程，マルコフ過程，拡散過程，マルチンゲールなどはもっともよく研究されている。
［ガウス過程］
　｛X_t(ω)｝を確率過程とする。…

※「ガウス過程」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」