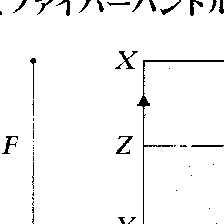ファイバーバンドル（その他表記）fibre bundle

改訂新版　世界大百科事典

ファイバーバンドル
fibre bundle

位相空間E，B，Fに対して，連続写像p：E→Bがあって，次の条件が成り立つとき，Eは，FをファイバーとするB上のファイバーバンドルであるといい，p：E→Bをその射影という。Bのどの点bについても，bの適当な近傍Uをとれば，UとFの直積U×FとpによるUの逆像p⁻¹（U）との間に，U×Fの各点（x，y）をp⁻¹（x）の上にうつすような同相写像が存在する。この条件はp：E→Bは局所的には（すなわち，Bの各点のある近傍上では）直積であることを意味している。

　例1　メービウスの帯上の各点に対し，その点より中心線に下ろした垂線の足を対応させる写像を考えれば，メービウスの帯は閉区間をファイバーとする円周上のファイバーバンドルとなる（図）。

　例2　n次元微分可能多様体M上のすべての点におけるすべての接ベクトルの全体をEとして，各接ベクトルにその始点を対応させる写像を考えれば，Eはn次元ユークリッド空間をファイバーとするM上のファイバーバンドルとなる。これを接バンドルという。

　Bの各点bに対し，p⁻¹（b）をb上のファイバーという。これはFと同相であるが，その間に標準的な同相写像があるわけではない。そこで，これらの同相写像に関するある条件を加えて，ファイバーバンドルの定義を上記のものより限定的に使うことがある。ファイバーバンドルの概念は接バンドルを起源として導入され，これにより微分可能多様体の理論が形成された。今日ではファイバーバンドルの概念は多方面で活用されている。
執筆者：中岡 稔

図－ファイバーバンドル

出典　株式会社平凡社「改訂新版　世界大百科事典」