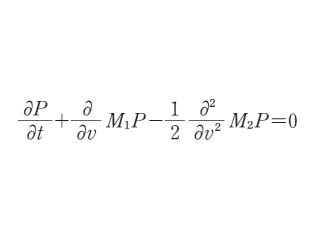フォッカー=プランク方程式（読み）フォッカー＝プランクほうていしき（その他表記）Fokker-Planck equation

ブリタニカ国際大百科事典 小項目事典

フォッカー＝プランク方程式
フォッカー＝プランクほうていしき
Fokker-Planck equation

マルコフ過程における確率密度関数の時間変化を表わす方程式。非平衡系を取扱う統計力学で，熱平衡への近づき方を表わすのによく使われる。ある量が時刻0に x という値をとったとき，時刻 t に y という値をとる確率を P(x;y，t) とし，0＜t'＜t のとき
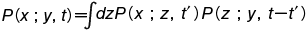が成り立つとする。 P の時間変化を支配するフォッカー＝プランク方程式はマスター方程式より導かれて次の形をとる。
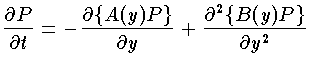この式は確率密度が時間とともにどう拡散していくかを教えてくれる。ただし A ，B は (x－y) ，(x－y)² の P(x;y，t) についての平均値に関する量である。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

フォッカー‐プランク方程式【Focker-Planck equation】

マルコフ過程＊の時間依存性を表現する方程式である．時刻ゼロの時点で速度 v₀ をもっていた粒子が，時刻 t で速度 v～v＋dv の間の速度をもつ確率を P（v，t |v₀）のように表すと，

ここに M_n＝（1/τ） 〈 [⊿v（τ）]ⁿ 〉（n＝1，2，…）であるが，[⊿v（τ）]ⁿ は時間 τ 内における速度の増分の n 次モーメントを表す．

出典　朝倉書店