統計力学（読み）トウケイリキガク（英語表記）statistical mechanics

デジタル大辞泉

とうけい‐りきがく【統計力学】

原子や分子の運動を統計的に取り扱い、それらの集まりである物質の巨視的な性質を説明しようとする理論的方法。用いる力学法則によって古典統計力学と量子統計力学とがある。統計物理学。

出典　小学館

精選版 日本国語大辞典

とうけい‐りきがく【統計力学】

1. 〘 名詞 〙 物質を構成する素粒子、原子、分子などの微粒子の運動法則をもとに、物質の巨視的性質・現象を、統計的・確率的に説明する物理学。運動法則に古典力学を用いる古典統計力学と量子力学を用いる量子統計力学がある。〔自然科学的世界像（1938）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

統計力学 (とうけいりきがく)
statistical mechanics

自然界には種々の物質があり，物質の性質が自然現象の起り方を決めている。人間は古代以来，物質構造についての仮説からその性質を説明しようと努力してきた。その理論の現在の形が統計力学，または統計物理学と呼ばれる学問分野である。統計力学は，ある構造をもつ物質はどのような性質を示すかを予言し，また，ある性質を示す物質はどのような構造をもつはずかという問いに答えて，構造の解明を助ける。

　物質は非常に多数の分子や原子，あるいはイオンや電子などから構成されている。この見方が物質構造の原子観である。例えば1辺1cmの立方体の食塩内にはそれぞれ2.2×10²²個の塩素イオンとナトリウムイオンが含まれている。また同じ体積で0℃，1atmの空気中には1.1×10¹⁹個の酸素分子，3.7×10¹⁹個の窒素分子などがある。これらの微小粒子は互いに力を及ぼしあいながら，非常に複雑な運動をしている。これを熱運動という。食塩結晶内の各イオンは10¹²～10¹³Hz程度にも及ぶ振動数で平衡点のまわりに振動しているし，空気中の窒素分子は450m/s程度の速さで飛行し，毎秒10¹⁰回くらい，他分子と衝突して進路を曲げる。このような高速でしかも複雑な分子運動を，莫大な数の分子のすべてについて詳しく測定，または計算で求めることは現在の人間の能力をはるかに超える。上述の空気について1秒間の全分子運動を記述するには10³⁰個以上の数値を要するが，現在，最大級の電子計算機の記憶容量10³～10⁴メガバイト（データ10⁹～10¹⁰個）にも格納しきれない。これらの数値を処理して物質の性質を算出することも人間の能力を超え，統計学の手法が必要となる。

　もちろん，この手法で求められる性質の種類には制限が生ずる。容器内の静止気体が器壁に及ぼす圧力と気体の温度，体積，分量との間の関係式をその気体の状態方程式と呼ぶが，この種の関係式を求めるのに統計学の手法が有効なのである。分子が器壁に衝突して反発されるとき器壁の受ける撃力が圧力の原因であるが，前述の空気では1cm四方の壁面に毎秒4×10²³個の撃力が加わり，個々の撃力の大きさは3×10⁻¹⁸dyn・s程度で非常に小さい。壁の1面の1mm四方の部分が圧力測定装置になっているとすると，それ自身が原子から組み立てられており，分子1個に比べ非常に大きい質量をもつので，自動車が凸凹道を走るとき車体は凹凸をならした形でしか上下振動をしないように，多数の撃力を分離しては測定できず，時間および壁面についてならした値のみを与える。その平均値を単位面積当りに換算したものが圧力の測定値である。

　このように原子分子の世界から見れば非常に巨大ではあるが，人間生活の尺度では微小とされる寸法の時区間，空間領域にわたって平均された物理量を巨視的物理量と呼ぶ。いくつかの巨視的物理量の間に成立する関係式で表現される性質を求めるには，すべての原子や分子について位置や速度などを知る必要はない。圧力の計算に必要な知識は，壁面単位面積当り単位時間につき，ある速さ，ある角度で衝突してくる分子の平均数である。これを求めるには気体内の分子をその速度によって組み分けし，ある速度のものが何個含まれているかを知ればよい。それは速度分布則で表される。このような統計的知識を与えること，また原子や分子の運動に伴って，速度分布則などが時間によってどう変化するかを原子や分子の従う力学法則に基づいて定めることが統計力学の任務である。

統計力学史

静力学的理論から動力学的理論へ

統計力学形成の歴史は物質構造認識の発展と分かちがたく結びついていた。1850年ころまで気体は構成粒子が互いに接しあって詰まっている構造をもつとされた。R.ボイルは粒子自身の弾性により圧力と体積の積が一定という法則（いわゆるボイルの法則）が理解されるとした。ニュートンは隣接2粒子間に中心間隔に反比例する遠隔斥力が働くとしてボイルの法則を静力学で説明した。現象から力を知り，その力から他の現象を数学的に厳密に推論するというのがニュートンの自然哲学の数学的原理であり，その力の原因については仮説を捏造（ねつぞう）すべきではないとした。しかし，ボイルやデカルトの機械論哲学では遠隔力も説明さるべき現象であった。ラプラスは原子には熱素の雰囲気があり，熱素は原子により放射吸収されるとし，ニュートンの斥力を放射平衡の条件から説明しようとした。ランフォードやH.デービーの実験も熱素説を否定できず，彼らの主張であいまいであった原子の運動も平衡点のまわりの振動や自転として取り込まれた。以上のような気体の静力学的理論では物質の対流以外に分子の並進運動は考えられておらず，この点が以下に述べる動力学的理論との根本的な違いである。

　原子を剛体球と考え，それらが真空中を自由に飛び回っているという構造仮説からボイルの法則を理解しようとする動力学的理論は，D.ベルヌーイ（1738），ヘラパスJohn Herapath（1821），ウォーターストンJohn James Waterston（1846）らが提出したが，ニュートンやラプラスの権威が学会を支配していた時代には，原子間力を無視する単純化しすぎた理論として受け入れられなかった。熱素説を崩したものは熱量則を否定した熱力学の成立であり，J.R.マイヤー，J.P.ジュール，H.L.F.ヘルムホルツによるエネルギー保存則とカルノーの定理の総合として，R.J.E.クラウジウス，W.トムソン（ケルビン）によって建設された。また，ジュールとヘルムホルツは種々のエネルギー形態のうち力学的エネルギーを根本的と考えた。これらの事情が力学への信頼を高め，1850年ころの動力学的理論復活への道を開いたという。

　動力学的理論の学界における復活は，まずクレーニヒAugust Karl Krönig（1822-79）によってなされた。彼は気体内の分子は定まった平衡点のまわりに振動しているのではなく，定速度で直線状の並進運動をしているとし，分子が対向する壁面間を往復するとして一壁面に衝突する分子数を求め，理想気体の状態方程式を導いた（1856）。クラウジウスは分子の並進運動だけでは比熱の測定値を説明するには不足であるとし，さらに分子が2個以上の原子からなり，分子の自転や内部振動があるとした（1857）が，このころには化学界でもS.カニッツァーロがアボガドロの仮説により多原子分子の考えを確定している。気体内の分子が毎秒数百mの平均速度で器壁間を往復するとすれば，室内のタバコの煙がゆっくり拡散するという日常生活の経験事実に反する。この異論に答えてクラウジウスは平均自由行路の概念を導入した（1858）。分子の飛行経路を曲げる分子間衝突を無視する計算が正しいのは，分子の平均自由行路λが分子間力の有効半径aに比べて十分に長い場合であるが，λは日常生活の尺度から見れば非常に短いために拡散は遅いのである。aの値が不明なのでλを計算できなかったが，ここにおいて動力学的理論にも分子間力が取り入れられたのである。クレーニヒの計算では分子は総数の1/3ずつが立方体容器の3稜に平行に往復飛行すると仮定したが，この仮定は直方体や球形の容器では妙な答えを与えるし，気体の等方性にも反する。クラウジウスは温度の関数の平均の速さですべての方向に同数ずつ飛行するとし，さらに器壁への衝突数を計算するため衝突数算出の仮定を導入した。

　J.C.マクスウェルは初め気体の動力学的理論は誤りだと思っていたという。ニュートン以来の伝統に従って，数学的問題として途中にかってな推測を交えず厳密に計算してみれば妙な答えが出て否定されると考えた。このため，彼は動力学的理論の検証を試みるのであるが，計算にあたって欠けている速度分布則には統計学からガウスの最小二乗法の誤差法則の形を借用した。分子の並進速度の直交3成分v_x，v_y，v_zは互いに独立な確率変数で同形の分布をもつとして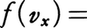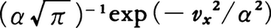，の形の分布則を得た。この速度分布則をマクスウェルの速度分布則と呼ぶ。彼は，各分子の運動はニュートン力学に従うとして，平均自由行程λ＝1/（\(\sqrt{2}\)πa²n），状態方程式p＝1/2nmα²を得た。ここでpは圧力，aは剛体球分子の直径，mは質量，nは数密度である。理想気体の状態方程式と比べ，α²は絶対温度Tに比例するとした。特殊な分子間衝突に限れば，衝突を繰り返すと運動エネルギーが分子間で等分配に近づき，先の分布則が成立するであろうことを示せた。マクスウェルは粘性が問題となる土星の輪の研究を経て動力学的理論に入ったので粘性に興味があった。動力学的理論に基づけば，粘性率はμ＝\(\sqrt{2}\)mα/（3π^3/2a²）と求まり，密度ρ＝mnによらない。これは最初にもくろんだとおり，既知の実験と矛盾する結論であった。静力学的理論では気体の粘性率は液体と同じく密度とともに増加するとされたのである。これによってマクスウェルは動力学的理論は誤りであると考えたのだが，その後マクスウェル自身によるものをも含めて実験が繰り返された結果，1865年ころまでには，逆に，静力学的理論は完全に否定され，動力学的理論こそ分子の寸法などを探る最有力の手段として学界に受容されるようになった。

　ここから歴史は二筋に分かれる。一方は動力学的理論を気体状態の時間的変化まで追う気体分子運動論の完成への道で，他方は気体とは構造の違う液体や固体にも適用できる熱平衡状態の統計力学への道である。

気体分子運動論

マクスウェルは平均自由行路理論から拡散係数と熱伝導率の計算を初めて与えたが，熱伝導と同時に起こる物質の流れを見落としていること，また温度，密度や平均自由行路も場所の関数とすべきことをクラウジウスに指摘された。マクスウェルは平均自由行路概念を動力学的理論の基礎には据えられぬことを見抜き，衝突数算出の仮定と衝突直前の2分子は互いに相関をもたぬという仮定を用いて，共存する輸送現象を統一的に取り扱う任意の巨視的物理量に対する一般的輸送方程式を導いた。分子を剛体球とする考えはやめ，ニュートン流に分子間力を距離rの－n乗に比例する斥力とした。ちなみに熱素説では分子間力は遠方で斥力，近距離で引力とされていた。n＝5の場合をマクスウェル分子と呼ぶが，この場合には輸送係数の計算式から分子間の相対速度を消去できるため速度分布則が不要となり，計算が実行可能となる。マクスウェルは，粘性率は圧力と密度の比に比例し，理想気体の状態方程式を使えば絶対温度Tに比例する結果を得た。前章で述べたように剛体球分子とした場合は粘性率はα，すなわち\(\sqrt{T}\)に比例していた。これに対してO.E.マイヤーはジュール=トムソン効果では分子間力は遠方で引力となるべきことを指摘し，また彼らの実験ではμ∝T^kのべき指数kは0.5と1の中間の0.65から0.96までに入った。マクスウェルの輸送理論は速度分布関数の時間変化を直接定める形には公式化されていなかった。熱平衡状態での形は，1860年の速度成分を確率変数とする仮定は根拠があやふやだと反省し，のちに分子間衝突で分布の形が変わらぬ条件を表す詳細に見たつりあいの式の解として求め直している。

　熱力学の第1法則は力学のエネルギー原理にほかならなかったが，L.ボルツマンは熱力学の第2法則を力学的に証明しようとして気体の動力学的理論に入ってきた。速度分布の初期の形がどうであっても時間の経過とともにマクスウェルの分布則に近づくことの証明が根本問題であった。ボルツマンはマクスウェルの独創的な輸送理論に感激し，72年，それと同じ手法で速度分布関数の時間変化を定める方程式を導いた。これをボルツマン方程式と呼ぶ。この非線形微積分方程式はマクスウェル分子に対しては解け，マクスウェルの結果と一致する粘性率と熱伝導率を得た（ただし，熱伝導率ではマクスウェルに計算違いがあった）。ボルツマンは第2法則の解析的証明として，極小値がエントロピーに比例する量E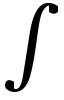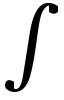＝……f logfdxdydzdv_xdv_ydv_zを発見し，気体が固定壁に囲まれているときE（H関数と呼ばれる）は時間とともに減少することを証明した。これをボルツマンのH定理といい，これによりボルツマン自身はエントロピーは増大するという第2法則は証明されたと考えた。ただし，Eはエントロピーとは符号が異なるので，のち，バーバリが文字EをHに変えた。

　ボルツマンには無限大や無限小は非物理的な極限概念としてしか意味をもたないとの思想があり，エネルギーは微小素量εの整数倍の値のみをとれるとして，ボルツマン方程式を連立常微分方程式に直し，その解やH定理を調べている。D.ヒルベルトは連立一次方程式を拡張して線形積分方程式論を作ったが，応用例としてボルツマン方程式に興味をもち，弟子に講義し研究を勧めた。講義を受けたD.エンスコクはマクスウェル分布から逐次に近似を上げて正常解と呼ばれるものを得る方法を発見，他方，S.チャップマンはマクスウェル分布からのはずれを分子の熱運動速度の多項式に展開する形を仮定し，マクスウェルの輸送方程式系を満たすように展開係数を求める方法を発見した。両方法で計算した粘性率，熱伝導率は一致し，のちにグラドによって両方法の同等性が証明されている（1958，63）。以上のような経過をたどって気体分子運動論が確立されたのである。

　なお，H定理に対しては1876年，ボルツマンの同僚のJ.ロシュミットは，ある瞬間に全分子の速度を逆転させると全事象の経過は逆行するはずであるから，H関数が減少する一方であることは力学法則だけからは結論できぬとの注意を与えている。これを可逆性の背理と呼ぶ。日常見られる現象を逆行させると，河川の逆流その他奇異なことになるが，当時唯物論者が似たような主張をしていたという。ボルツマン自身もH関数を増加させる初期条件もあることを認めたが，そのような初期条件は例外的だとしたいので，H関数の減少する確率が高いという形でしか証明の道はないと考えた。
→気体分子運動論

エルゴード仮説と統計集団

熱平衡状態の統計力学の建設はすんなりとはいかなかったが，1868年にボルツマンが，分子の速度成分を確率変数とみるマクスウェルの速度分布の導出法は分子運動がニュートン力学に従うことと矛盾するとし，気体分子間のエネルギー分配問題を考え直したところから始まる。ボルツマンは，気体内の1個の分子に着目すると，そのエネルギーは他分子との衝突により増減するが，単位時間中に区間（A，A＋dA）内のエネルギー値をとる状態に滞在する割合としてエネルギー分布則Φ（A）dAを定義する。Φ（A）の形は詳細に見たつりあいの式の解としてΦ（A）∝e⁻^haと求まる。hは絶対温度に反比例する定数である。この方法はポテンシャルをもつ外力が分子に作用している場合へも拡張できて，Aは分子1個の運動エネルギーにポテンシャルエネルギーを加えたものとすればよい。このようにして得られた熱平衡状態における分子の各状態の確率分布をマクスウェル=ボルツマン分布と呼ぶ。ボルツマンはさらに分子間衝突を具体的に取り扱わなくてよい一般論に触れている。この新方法は71年に詳しく公式化され，まず数式変形のための補助概念としてのちにマクスウェルが統計集団と呼ぶものを導入する。気体で分子間相互作用をなくすると計算が楽になるように，互いに相互作用をしない同形で初期条件のみ異なる力学系の集合（統計集団）を考え，ある時刻にある状態に存在する系の個数の割合としてその状態の見いだされる確率を考える。そして計算結果を滞在時間の割合で考えた式に戻すために，のちにエルゴード仮説と呼ばれる仮説を使う。このエルゴード仮説というのは，熱運動は非常に不規則であり，また種々雑多な外力が作用するので，物体中の原子はエネルギー保存則と両立するすべての可能な位置と速度とを熱運動によって一巡するという仮説である。この仮説は証明されていないがボルツマンはもっともらしいとした。これによると統計集団での平均と滞在時間による長時間平均とは一致する。これをエルゴード定理と呼ぶ。ボルツマンはこの方法でマクスウェル=ボルツマン分布をJ.W.ギブズが正準分布と呼ぶものへと拡張したのであるが，マクスウェルが79年に取り上げるまで，この新方法も顧みられなかった。
→エルゴード理論

マクスウェルの魔物

マクスウェルは熱力学の第2法則は数学的真理ではなく統計的真理であるとした。このことに関連して彼は各分子の走路を追跡できる鋭い能力をもつ生物を想像する。この生物が空気の入った2室A，Bを隔てる壁の小孔を開閉させ，高速分子はAからBへ，遅速分子はBからAへ通過させれば，仕事の消費なしにBの温度を上げAの温度を下げられるので第2法則は破られることになる。これがマクスウェルの魔物と呼ばれるものである。イギリスではこの議論は受容され，第2法則の議論は20年間くらいやんだ。マクスウェルはまた，異種の分子を混合するとエントロピーは増すのに同種のときは不変であるというギブズの背理を考え，エントロピーは系自体のもつ観測可能な性質ではなく，系についての人間の知識にも関係する量だとした。つまりエントロピーは微視的物理量ではなく，巨視的物理量だというのである。

ボルツマン=プランクの方法

1877年，ボルツマンは第2法則の確率論的基礎付けを追う途上で，以下に述べるような熱平衡状態のまったく独特な決定法を発見した。非常に多数の微視的状態は巨視的物理量で指定される同一の巨視的状態に見えるが，巨視的状態によって対応する微視的状態の個数が異なり，熱平衡状態に対応する個数は非平衡状態に対応するものに比べ圧倒的に大きい。エルゴード仮説で微視的状態を一巡する間にある巨視的状態に滞在する時間の割合は，対応する微視的状態の個数に比例するであろう。自然界に現れるすべての無限は，極限移行以外の何物でもないから，分子の速度も有限個の離散値のみをとると考える。n個の分子を含む気体の微視的状態は，n個の速度値で指定されるが，巨視的状態は各速度値をそれぞれ何個の分子がもつかという速度分布の形で指定される。長時間平均を測定値とすると各時点，したがってエルゴード定理により各微視的状態は等しい重みをもち，各巨視的状態は対応する微視的状態の個数に比例する確率Wをもつことになる。Wの自然対数logWは分子数が大きい漸近的極限でH関数に負号をつけたものに比例するので，エントロピーSと同一視することができる。この新方法もまた1900年にM.プランクが取り上げるまでは気体運動論者たちから無視され，議論されたのは依然としてH定理であった。

　プランクの助手E.ツェルメロは，有界な力学系は有限時間内に出発状態の近傍へ必ず戻るというポアンカレの再帰定理に基づいて，一方向に進行する不可逆過程は不可能であり，最大確率状態へ向かう変化が起こるというH定理の新解釈を否定した（1896）。これを再帰性の背理と呼ぶ。ボルツマンは，H関数の値を時間に対して描いたH曲線は大多数の初期条件に対しほとんどつねに極小値付近にあり，たまに高い隆起を示すと考えていた。これは再帰定理と調和する。しかし，初期状態が非常に高い隆起上にあれば大きな確率をもって極小部に近づけられ，非常に長時間はそこから無視しうるほどわずかしか離れない。ボルツマンは再帰時間をエルゴード仮説から評価したが，それによれば10¹⁸個の分子を含む1cm³の気体の状態を分子の位置は10⁻²¹cm³，速度は1m³/s³の立方体内に1個の値をとるとして区別するとき，初め分子の速さが500m/sである状態に，各分子が毎秒4×10⁹回の衝突を受けるとして，再帰する時間は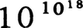年となった。ちなみに最近の宇宙年齢の推定値は1.55×10⁹年である。ボルツマンの思想によれば，起こらないというのは極端に起こりにくいことの極限に過ぎない。しかし，ツェルメロはH曲線の隆起の下降側と同様に上昇側に初期状態をとれると反論し，ボルツマンは小確率の状態から大確率の状態へ進む方向で時間の流れを定義すべきであるとの考えへ追い込まれた。E.マッハもエントロピーの増大量の測定が時間の絶対測定だと主張していた。つまり現在の宇宙は第2法則の成立する方向に進行しているわけである。

　プランクは学位論文に第2法則を選んだが，過程を重視したクラウジウスに対し，状態を基礎に据えた。プランクは有限自由度の分子系では第2法則の力学的証明はできないが，連続自由度をもつ系ならマクスウェルの魔物も作用しないから証明可能かもしれぬというヘルムホルツの講義を聞いており，熱力学の適用できる電磁場，すなわち熱放射の研究に入った。マクスウェルの電磁場の基礎方程式（マクスウェルの方程式）で電荷や電流はまだ場の量であった。これらが物質の電荷によるという考えは，すでにH.A.ローレンツの電子論が与えていたが，プランクは1896年，場の量である微小振動電流として共鳴子を導入し，放射減衰方程式を導出した。これは特殊な初期条件を選んだ結果であるとボルツマンに注意され，気体分子運動論の分子無秩序の仮説をもち込む。ボルツマンによるこの仮説では，分子の位置や速度に離散値を与えるとき位置空間や速度空間を微小立方体に区分し，各立方体内には多数の分子を所属させるが，各分子は同一，あるいは他の立方体に属する分子とは相関をもたないとする。この仮説は衝突数算出の仮定の基礎であるが，初期状態での成立を前提としても，ボルツマン方程式やH定理の証明に必要な以後のすべての時刻に対する成立は力学からは保証されない。これについてボルツマンは平均自由行路が分子間隔に比べて長いなら保証が得られるとした。同時代人は分子無秩序の仮説の成立せぬ微視的状態は自然界には起こらぬことと受け取った。プランクは観測される巨視的電磁場の時間変化を追うときつごうの悪い微視的場は起こらぬという自然な放射の仮定をしたが，これは第2法則の微視的成立を信じたためである。

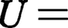
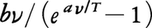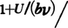
　プランクは放射減衰方程式から第2法則を証明するため，振動数ν，エネルギーUをもつ共鳴子のエントロピーをH関数との類推でS＝－（U/aν）｛log（U/bν）－1｝の式で定義した。U/aνのみの関数となることはウィーンの変位則による。∂S/∂U＝1/Tからウィーンの放射式U＝bνexp（－aν/T）を得，a，bは普遍定数となる。この放射式は高振動数側ν→∞では実験とあうから，U→0で∂²S/∂U²＝－（aνU）⁻¹はよいが，低振動数側ν→0では測定値と40～50%の食違いを生じ，むしろU→∞で∂²S/∂U²∝－U⁻²となることが判明した。プランクは（∂²S/∂U²）⁻¹をUの二次式で内挿し，∂S/∂U＝1/Tからプランクの放射式を得た。実験とよくあったが，問題はそれを与えるエントロピーの形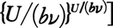を一義的に与える基礎である。熱力学ではだめで，キルヒホフの遺稿整理を通じて注意深く研究していたボルツマンの定義S＝（b/a）log R＋const.しかなかった。ただし，付加定数は無視する。共鳴子N個が独立に放射場と熱平衡にあれば，NU＝Pε，ε＝bνととると，エントロピー式で［　］内は（N＋P）ⁿ⁺^p/（NⁿP^p）と書け，R＝（N＋P－1）！/｛（N－1）！P！｝のN≫1，P≫1のときの値となり，普遍定数はk＝b/a＝1.346×10⁻¹⁶erg/degとh＝a＝6.55×10⁻²⁷erg・sと求まった。RはP個のε＝hνをN個の共鳴子に重複を許して配る方法の数であるが，その物理的説明は難解で，プランクが詳しく説明し直し（1906），ローレンツがボルツマンの気体論と同形に書けることを示した（1910）。かくしてウィーン市のボルツマン記念碑に彫られている式S＝klogWが1910年ころヨーロッパの学会に受容された。この式をボルツマンの原理と呼び，それに基づく計算法をボルツマン=プランクの方法という。しかし，RまたはWの計算は気体のような互いに独立な要素からなる系でしか実行可能でない。
→エントロピー

ギブズの統計力学

マクスウェルは分子運動論から液体や固体に適用できぬという限界を取り除く巧妙な満足のいく方法として，ボルツマンの結果をハミルトン形式の力学を用い，統計集団を基礎に据えて統計的記述に書き直した（1879）。集団に属する系がある微視的状態に見いだされる確率分布の決定が統計的方法の目標であるが，孤立した物質系に対し，リウビルの体積不変定理によって定常解の一つとしてギブズが小正準分布と呼ぶものを見いだしている。その際，エルゴード仮説を使って分布の形を決める代りに，初期分布の形についての仮定を用いた。エルゴード仮説を，系は自然運動の経過としてエネルギー保存則と矛盾しないすべての微視的状態を通過するという形で述べているが，その正否は未解決としている。ボルツマンの記述にあった熱運動の不規則性は，分子運動自体は本来そのようなものではなく，人間の受取り方だとの考えから除かれている。外力の多様性については，容器壁などの固定障害物の表面が特殊の形をもたない限り，各分子の衝突により系の運動に乱れが生ずると具体化されている。小正準分布以外に定常分布がないか否かは未解決だが，第2法則という経験事実によれば唯一の分布となるとしている。エルゴードなる名称はボルツマンが導入したもので，土星の輪のように系がびっしり並んで流れているエネルギー面上の道の意であり，小正準集合に当たる。ボルツマンはただ1個の系の状態変化を追う自分の方法は集団の分布の変化を追うマクスウェルの方法とは違うと主張したが，1887年には集団の方法を受け入れた。

　熱力学の研究で優れた成果をあげたアメリカのギブズも統計集団を考え，確率保存則を表すリウビル方程式を導出することで分子運動論に入ってきた。位置座標と速度の組を用い，正準運動量は使っていない。講義してはいたが，完全と信ずるまで論文発表をしないギブズは，熱力学との類似物を探す方針で，先人たちの成果をもっとも論理的に配列し直して集大成した。この理論体系をギブズの統計力学と呼ぶ。熱力学同様に物質構造の仮説に依存しない一般的な公式化が必要であった。比熱問題にみられるように物質構造の仮説を立てることはきわめて困難であったし，これを放棄すれば仮説の誤りに基づく理論の崩壊も生じない。ここで初めて理論体系は構造仮説と切り離された。ギブズはボルツマン=プランクの方法のように熱力学の式と混用するのではなく，熱力学とは独立に理論を展開することにより，熱力学の法則は系に含まれる粒子数が非常に多いときの近似的なもっとも確からしい挙動を与えることを示そうとした。つまり個々の粒子に関する量の程度までは精度不足で認識できず，またもっとも確からしい結果以外を得るほど多数回の測定ができない生物にみえる力学法則が熱力学の法則だという。理論はマクスウェルのいう統計的なものとなる。統計集団を考える数学的利点は，集団中には例外的な初期条件に相当する系は無視できる割合でしか含まれぬことにある。統計力学の法則は任意の大きさの自由度をもつ保存系に適用され，正確であるという。自由度nの系の微視的状態は，一般化座標q₁，q₂，……，q_nおよびこれらに正準共役な運動量p₁，p₂，……，p_nによって指定する。ある時刻tにこれら2n個の量がとる値の組を系の位相と呼び，可能な位相の集合である2n次元ユークリッド空間を位相空間という（この位相空間をP.エーレンフェストはΓ空間と呼んだ）。この空間内の確率分布ζ（q₁，……，q_n，p₁，……，p_n，t）の形で統計集団が規定される。つまり位相空間を体積⊿Γの微小部分に分割し，ある微小部分に属する位相をもつ系の個数を集団に含まれる系の総数で割り，さらに⊿Γで割った量で，系の総数無限大の極限をとり，⊿Γ→0の極限をとって得られるものをその微小部分に相当する確率密度ρとする。ただし，規格化条件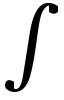……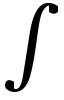ρ（q₁，……，p_n，t）dq₁……dp_n＝1を課してある。定常な確率分布をもつ統計集団が熱平衡にある系に対応するが，その分布の形は天下りに与えた。保存系ではエネルギーが不変なので，系のハミルトニアンのみを通して位相に依存する分布は定常である。もっとも解析的に取り扱いやすいものが正準集団で，確率分布はρ＝exp｛（F－）/kT｝の形をもつ。kはボルツマン定数，Tは熱力学関係式との比較から絶対温度と解釈される。規格化因子Fはヘルムホルツの自由エネルギーに当たるが，exp｛－F/kT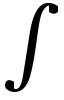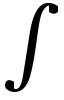｝＝……exp｛－/kT｝dq₁……dp_nから求められる。この式の右辺の積分をプランクは状態和，ファウラーは分配関数と呼んだ。孤立保存系に対応する意味でもっとも簡単で自然なものは小正準集団で，位相空間の2枚の等エネルギー面＝E，＝E＋⊿Eに挟まれる部分内で一定値をとり，その外部で0となる分布の⊿E→0の極限形で規定される。種々の物理量の平均値やゆらぎが計算されていて，ゆらぎは平均値からのはずれの平方の平均値で定義され，系に含まれる粒子数が非常に大きいとき平均値の平方に比べて無視できるが，ゆらぎまで計算できる点が熱力学より精密になっている。保存系では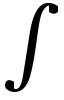……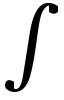ρ log ρ dq₁……dp_nは不変である。しかし，ρの定義で⊿Γ→0の極限をとる前の値をPとすると，すべての微小部分についての和ΣP log Pはt→±∞の極限をとった後で⊿Γ→0とすると最低値をとる。これがギブズのH定理である。微視的密度ρのときは先に⊿Γ→0とするからt→±∞でも値を変えなかった。極限の順序が問題になることは第2法則，あるいはエントロピー概念が人間の自然認識のしかたに依存することを示す。ギブズがボルツマンの原理による公式化を避けた理由であろう。さらにギブズは新しい統計集団として，粒子数の変動する系の取扱いに便利な大正準集団を導入した。

　同時代人にはギブズの統計力学は抽象的で理解困難であった。マクスウェルの後継者たちも統計集団を弱い相互作用をする同種の系の集合と誤解しており，この誤解は1930年代まで散見される。しかし，アインシュタインはギブズの統計力学とほぼ同じ理論を独力で作り上げた（1902-05）のみならず，熱力学そのものにゆらぎを導入し（1906），ボルツマンの原理の内容を転倒してエントロピーから熱力学変数のゆらぎの確率分布がW＝exp（S/k）で与えられるとした（1907，10）。ニュートンの光粒子説の再提唱と誤解された光量子仮説などにより，アインシュタインは過激とみなされており，統計力学の仕事はほとんど無視されていたが，物理化学分野のH.W.ネルンストが熱力学の第3法則を発見し（1905），比熱は絶対0度で0となることを示すと，プランクの熱放射式をエネルギー等分配則の代りに用いるアインシュタインの固体比熱理論（アインシュタインの比熱式）は注目され，またコロイド粒子のブラウン運動は熱運動であることを予言したアインシュタインの理論は，J.B.ペランたちの実験で検証された。

　熱力学の近似性，すなわち巨視的性格は学会に承認された。1910年までで熱放射問題はだいたい片づき，11年からは第3法則に関連して比熱問題が興味の中心にきた。原子スペクトルの問題とともに分子内部運動量子化の必要性が広く認められ，プランクやゾンマーフェルト=ウィルソンの量子化条件式の提唱を経て，25年ころに古典力学が量子力学で置き換えられた。さらにフォン・ノイマンによりΓ空間の確率密度ρは密度行列，あるいは統計演算子に置き換えられた。このときギブズの統計力学は完璧に量子力学に翻訳されて，量子力学に基づく量子統計力学に変貌できたために，ボルツマン=プランクの方法はとって代わられることとなった。30年代初頭には原子分子の内部構造や分子間力もだいたい明らかとなり，興味の中心は固体，とくに相転移問題に移る。なお，E.A.グッゲンハイムは物理化学向けに熱平衡状態の統計力学を統計熱力学と名付けた（1939）。
→量子統計

非平衡状態の統計力学

熱平衡状態から不可逆過程，あるいは輸送現象をも取り扱えるように統計力学を拡張することは1950年代に行われた。松原武生の温度グリーン関数法，久保亮五の線形応答理論，ボゴリューボフ=ティアブリコフの多時間グリーン関数法によって熱平衡に近い非平衡状態まで含む理論体系が確立した。このほか，森肇によりブラウン運動論の量子統計力学的公式化がなされている。
執筆者：橋爪 夏樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

統計力学
とうけいりきがく
statistical mechanics

熱力学は本来、系全体のマクロな性質を扱うが、それをミクロな古典力学あるいは量子力学的情報から導き出す理論が統計力学である。熱力学では、熱平衡状態におけるマクロな物理量（状態量）に関する基本関係式を求めることができるが、物質に固有な性質に関するいわゆる状態方程式に関してはあらかじめ知られた関係として与えなくてはならない。系のミクロな情報、おもにハミルトニアンから熱平衡状態での状態方程式を導くのが統計力学である。

　統計力学の始まりは気体分子運動論である。気体内の分子の速度分布を初めて求めたのはマクスウェルであるが、ボルツマンは気体が自ら熱平衡状態へ向かうという不可逆現象をH関数の減少によって説明した。この論の是非をめぐる議論によって、不可逆現象が統計性に由来することが明らかになり、エントロピーという量の微視的意味づけが確立された。

　このように力学的な運動を考え、その定常状態として熱平衡状態を記述する試みに対し、ギブスによってアンサンブル理論が導入された。これは、等重率の原理とよばれる、等エネルギー状態の出現確率が等しいとする原理に基づき、多くの同等な系を考え、その集団での平均をもって熱平衡状態の期待値とする考え方である。この理論の正当化には、エルゴード仮説など位相空間での平均と観測の関係が重要になる。外界から孤立し、エネルギーが保存された系を扱うミクロカノニカル集団では、等エネルギー状態にある状態数W(E)の対数がエントロピーになっていることがわかる。

S(E)＝k_BlnW(E)
この関係はボルツマンの原理とよばれ、統計力学の基礎的性質である。また、温度が決まっている熱源とエネルギーのやりとりがある場合の系のとりうる状態の集団はカノニカル集団とよばれる。そこではエネルギーE_iをもつある一つの状態の出現確率は、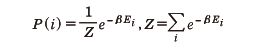

で与えられる。ここで、Zは規格化定数で分配関数とよばれる。

　さらには化学ポテンシャルが与えられた粒子源と粒子のやりとりがある場合のグランドカノニカル集団などがある。そこで、粒子数Nをもつある状態iの出現確率は、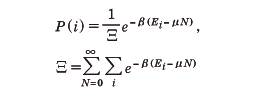

で与えられる。ここで、Ξ(クシー)は規格化定数で大分配関数とよばれる。

［宮下精二］

不可逆過程の統計力学

統計力学は、熱平衡状態の性質を微視的な情報から求める手法であるが、より一般に、多数の変数が集団としてみせる現象も研究の対象になっている。熱力学第二法則は、熱の流れる方向を規定しているが、その流れ方については何も示していない。そのため、熱平衡状態にどのように緩和していくのかは未知の問題である。ボルツマンのH定理は、この問題に真っ向から取り組んだものであるが、一般化はむずかしく、通常は平衡状態に関してはアンサンブル理論によって取り扱われている。しかし現在、その緩和の問題が、非平衡統計力学の問題として盛んに研究が進められている。

　粗視化による非平衡現象の把握に成功した例として流体力学がある。また、平衡に近い場合の線形応答理論（久保理論）は輸送現象などの解析で成功している。さらに、ブラウン運動の記述で導入されたランジュバン方程式や、分布関数の時間発展に衝突現象を考慮したボルツマン方程式など、さまざまな方法が考案されている。

［宮下精二］

[参照項目] | H定理 | エルゴード性 | エントロピー | 気体分子運動論 | ギブス | 久保亮五 | ハミルトニアン | 不可逆変化 | ブラウン運動 | ボルツマン | ボルツマン定数 | マクスウェル

出典　小学館　日本大百科全書(ニッポニカ)

化学辞典 第2版

統計力学
トウケイリキガク
statistical mechanics

物質の巨視的状態は，物質を構成するきわめて多数の微視的粒子(分子，原子，電子，原子核など)の性質および運動の総合的結果である．微視的要素の運動は，原理的には力学の法則によって記述される．この微視的世界の力学に立脚して，確率論的に巨視的世界の法則を導き出す理論的方法が統計力学である．とくに，熱平衡状態にある系に対しては，明確な理論が確立され，熱力学的現象を微視的立場から完全に説明することができる([別用語参照]統計熱力学)．統計力学は，気体分子運動論にその萠芽がある．L. Boltzmannは気体分子に対する速度分布則の一般的証明のために，H定理を導き，さらにエルゴード仮説のうえにエントロピーSの統計力学的意味を示すボルツマンの原理，

S(N,V,E)＝klog W
を与え，統計力学の創始者となった．ここで，kはボルツマン定数，Wは，粒子総数N，体積V，エネルギーEで指定された系が熱平衡状態で許される微視的状態の数を表す．Boltzmannに対して，J.W. Gibbs(ギブズ)は統計熱力学をさらに明確にした統一的な理論体系を建設した．これをGibbsの統計力学とよぶこともある．この方法は，のちにR.H. Fowlerらによって発展させられた．とくに，Gibbsが名づけたカノニカル集合は一定温度の熱源のなかに存在する統計集団を表現するもので，きわめて重要である．BoltzmannおよびGibbs時代の統計力学は，古典力学にもとづいているので，古典統計力学とよばれる．今日の統計力学は，本質的に量子力学にもとづく量子統計力学であって，古典統計力学は，その近似として成立する．非平衡状態に対する統計力学は，まだ簡明な統一的理論体系となっていない．代表的なものとしては，気体分子の位置・速度に対する確率分布の従う方程式を運動論的に解く方法，たとえばS. ChapmanおよびD. Enskogによる気体の輸送現象の理論がある．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

統計力学【とうけいりきがく】

統計物理学とも。物質を構成する無数の粒子（分子，原子など）の性質・行動を確率論的に処理することによって巨視的な諸現象を説明しようとする物理学の一部門。気体分子運動論に始まり，ボルツマンとギブズにより体系が確立された。統計力学によって，巨視的な熱力学理論が微視的な立場から根拠を与えられ，さらに熱力学が扱えなかった非平衡現象（拡散，粘性，電気伝導等）の研究も可能になった。量子力学の成立とともに粒子の運動法則を従来の力学から量子力学におきかえた量子統計力学が生まれ，古典統計力学はその近似と考えられるようになった。
→関連項目位相空間（物理）｜熱力学｜ボルツマン定数

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

統計力学
とうけいりきがく
statistical mechanics

統計物理学ともいう。物質を構成する多数の粒子の運動に力学法則および電磁法則と確率論とを適用し，物質の巨視的な性質を統計平均的な法則によって論じる物理学の分野。これにより巨視的世界と微視的世界とが結ばれる。気体の巨視的性質を気体分子の運動によって説明した分子運動論に始り，J.C.マクスウェル，L.ボルツマンが分子の速度分布，エネルギー分布を導入，J.ギブズが統計集団の考えを導入して熱平衡状態の統計力学を完成し，熱力学の微視的な基礎づけを与えた。これは統計熱力学とも呼ばれ，比熱，熱放射，相転移，誘電率，磁性など静的な性質を扱うものである。一方，状態の時間的変化に関係した輸送現象や拡散現象などの動的な性質を論じるものとして，気体の粘性や熱伝導に関する分子運動論を出発点として，非平衡状態の統計力学が展開されている。またブラウン運動や熱雑音のようなゆらぎ現象が，統計的平均からのずれによって起る確率過程として統計力学で論じられる。さらに微視的世界を支配する力学として量子力学が確立され，粒子集団に対するフェルミ統計，ボース統計が明らかとなり，これらを基礎とする量子統計力学が展開され，金属電子論や極低温の量子液体など物性物理学の一層の発展に寄与している。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

統計力学

「熱力学」のページをご覧ください。

出典　(株)朝日新聞出版発行「知恵蔵」