リーマンのゼータ関数（読み）リーマンノゼータカンスウ（その他表記）Riemann zeta function

デジタル大辞泉

リーマン‐の‐ゼータかんすう〔‐クワンスウ〕【リーマンのゼータ関数】

⇒ゼータ関数

出典　小学館

ブリタニカ国際大百科事典 小項目事典

リーマンのゼータ関数
リーマンのゼータかんすう
Riemann zeta function

級数 ζ（s）＝1＋1/2^s＋1/3^s＋…＋1/n^s＋… は，s＞1 のときに収束するが，ゲオルク・フリードリヒ・ベルンハルト・リーマンはこれを，s が複素数の場合に拡張して考察したので，これをリーマンのゼータ関数（またはジータ関数）という。リーマンは ζ（s）（s＝σ＋ti）の実数でない零点は，すべて σ＝1/2 という直線上にあると予想した。これはリーマンの仮説と呼ばれている。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のリーマンのゼータ関数の言及

【解析的整数論】より

…例えば，L.オイラーは次のような関数を考えた。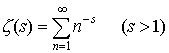これは，後にG.F.リーマンがこの関数について深い研究をしたので，リーマンのゼータ関数Riemann zeta functionと呼ばれている。オイラーはζ(s)について，いくつかの重要な発見をしたが，その一つとして次の無限積によるζ(s)の表示式を見いだした。…

※「リーマンのゼータ関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」