オイラーの方程式 (オイラーのほうていしき)
Euler's equation
y=y(x)が未知関数であって,x,y,y′の関数F(x,y,y′)が与えられているとき,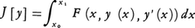 の値を最小にする問題(変分法)を考える。ただし,未知関数y(x)は境界条件のy(x0)=y0,y(x1)=y1をみたすものとする。いま,端点x0,x1で0になる任意の関数z(x)とパラメーターεとをもって,関数族Yε(x)=y(x)+εz(x)を考えると,y(x)がJ[y]の最小値を与える関数ならば,εの関数J[Yε]はε=0に対して最小になる。そこで,上記の積分の式で
の値を最小にする問題(変分法)を考える。ただし,未知関数y(x)は境界条件のy(x0)=y0,y(x1)=y1をみたすものとする。いま,端点x0,x1で0になる任意の関数z(x)とパラメーターεとをもって,関数族Yε(x)=y(x)+εz(x)を考えると,y(x)がJ[y]の最小値を与える関数ならば,εの関数J[Yε]はε=0に対して最小になる。そこで,上記の積分の式で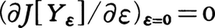 という条件を書き上げると,境界条件と部分積分により,
という条件を書き上げると,境界条件と部分積分により,
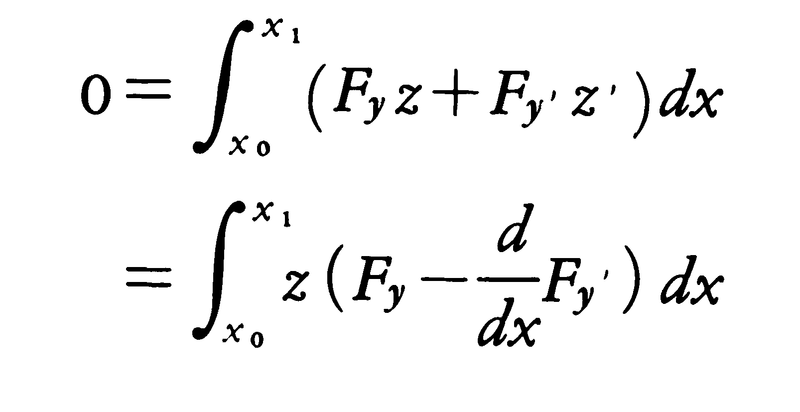
となる。ここで関数z(x)の任意性により,
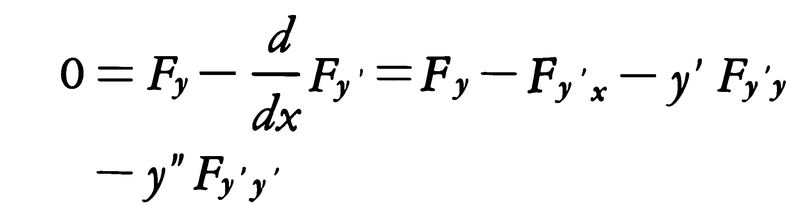
を得る。これをオイラーの方程式またはオイラー=ラグランジュの微分方程式という。この方程式は一般にyに関して2階の常微分方程式であるから,境界条件によって一つの解が定まる。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
法則の辞典
「オイラーの方程式」の解説
オイラーの方程式【Euler's equation(fluid dynamics)】
「オイラーの流体運動方程式」のページをご覧ください。
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のオイラーの方程式の言及
【運動方程式】より
…1点を固定した剛体の回転運動は,瞬間的に三つの座標軸Ox,Oy,Ozのまわりの回転運動を合わせたものと見なせるので,剛体の角運動量も力のモーメントもベクトルL,Nに置き換えて運動方程式として,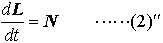 を得る。回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。
を得る。回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。[回転運動](c)流体の運動方程式 流体の場合も,その微小部分に着目することによって,(1)の運動方程式から流体に対するラグランジュの運動方程式またはオイラーの運動方程式を導くことができる。…
【変分法】より
…これを(3)に適用し,条件(2′)を使って部分積分を行うと,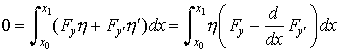 となるから,ηが(2′)を満たす関数の中では任意であることにより,
となるから,ηが(2′)を満たす関数の中では任意であることにより,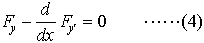 でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…
でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…
【ラグランジュ関数】より
…その結果,運動法則を個々の場合に応じて(1)の形に述べる代りに変分原理(2)によって統一的に示すことができるという利点が生ずるわけである。変分原理(2)から運動法則(1)が導かれるような関数L(x,x,t)が,運動方程式(1)のラグランジュ関数と呼ばれるものであり,変分法の一般論からその場合の運動方程式はオイラーの方程式,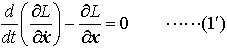 である。J.L.ラグランジュは最初いわゆる等周問題についてこの方程式を考察し,次いでニュートンの運動方程式に適用して解析力学の基礎を築いた。…
である。J.L.ラグランジュは最初いわゆる等周問題についてこの方程式を考察し,次いでニュートンの運動方程式に適用して解析力学の基礎を築いた。…
※「オイラーの方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
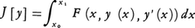 の値を最小にする問題(変分法)を考える。ただし,未知関数y(x)は境界条件のy(x0)=y0,y(x1)=y1をみたすものとする。いま,端点x0,x1で0になる任意の関数z(x)とパラメーターεとをもって,関数族Yε(x)=y(x)+εz(x)を考えると,y(x)がJ[y]の最小値を与える関数ならば,εの関数J[Yε]はε=0に対して最小になる。そこで,上記の積分の式で
の値を最小にする問題(変分法)を考える。ただし,未知関数y(x)は境界条件のy(x0)=y0,y(x1)=y1をみたすものとする。いま,端点x0,x1で0になる任意の関数z(x)とパラメーターεとをもって,関数族Yε(x)=y(x)+εz(x)を考えると,y(x)がJ[y]の最小値を与える関数ならば,εの関数J[Yε]はε=0に対して最小になる。そこで,上記の積分の式で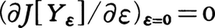 という条件を書き上げると,境界条件と部分積分により,
という条件を書き上げると,境界条件と部分積分により,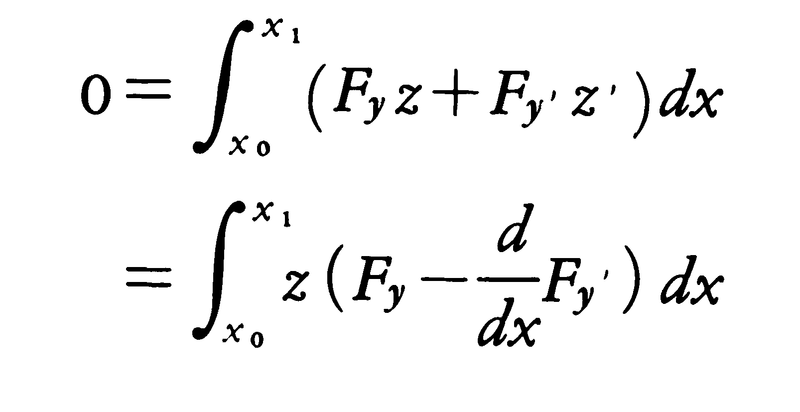
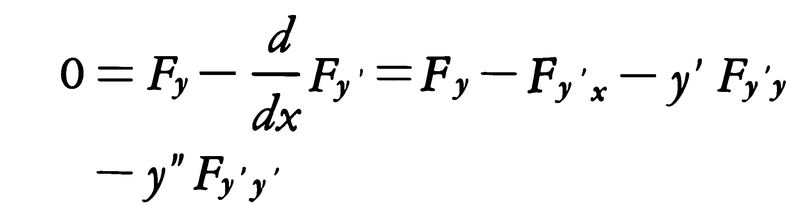


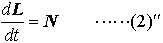 を得る。回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。
を得る。回転運動を剛体に固定した座標系,とくに慣性の主軸に選んでやれば,(2)″はオイラーの方程式と呼ばれるものになる。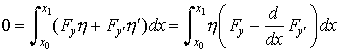 となるから,ηが(2′)を満たす関数の中では任意であることにより,
となるから,ηが(2′)を満たす関数の中では任意であることにより,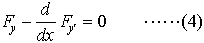 でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…
でなければならない。これをオイラー=ラグランジュの微分方程式,またはオイラーの方程式という。この方程式を満たす関数y(x)のうちで実際に(3)を最小にするものを求めればよい。…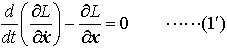 である。J.L.ラグランジュは最初いわゆる等周問題についてこの方程式を考察し,次いでニュートンの運動方程式に適用して解析力学の基礎を築いた。…
である。J.L.ラグランジュは最初いわゆる等周問題についてこの方程式を考察し,次いでニュートンの運動方程式に適用して解析力学の基礎を築いた。…