変分法（読み）ヘンブンホウ（英語表記）calculus of variations

デジタル大辞泉

へんぶん‐ほう〔‐ハフ〕【変分法】

ある未知の関数とその導関数を含む定積分として表される値を、与えられた条件の下で最大または最小とするような関数を求める方法。解析力学において用いられる。

出典　小学館

精選版 日本国語大辞典

へんぶん‐ほう ‥ハフ【変分法】

〘名〙 ＝へんぶんがく（変分学）〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

変分法
へんぶんほう
calculus of variations

微分法で取り扱われる極値問題は、ある領域内を動くn個の変数(x₁,x₂,……,x_n)の関数f(x₁,x₂,……,x_n)の最大値、最小値を求めるのに対し、変分法では、次の有名な例（1696年、J・ベルヌーイによる）のような問題を考える。

　垂直なx-y平面の二点A=(x₀,y₀),B=(x₁,y₁),x₁＞x₀,y₁＞y₀を滑らかな曲線y=(x)で結び、この曲線に沿って一つの球を摩擦を受けることなく滑り落とすとき、点Bへ最短時間で到達する曲線を求めよ。

　これを数式で表すには、曲線y=(x)に沿っての粒子の速度は、

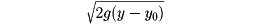
（落下した垂直距離の平方根、gは重力の加速度）に比例することを思い出すと、所要時間は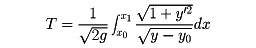

となる。本質的でない定数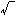（2g）やy₀を略すと、(x₀)=0,(x₁)=y₁となる連続微分可能な曲線y=(x)のうち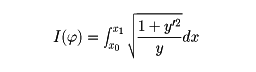

を最小にする(x)を求めよ、という問題になる（この解はサイクロイドである）。

　このように、関数(x)の実数値関数I()を最小にする(x)を求めよ、という形の問題を解くのが変分法である。

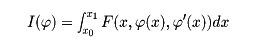
のとき、(x)=u(x)で最大、最小をとる必要十分条件は、オイラーの方程式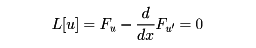

を満足することである。

　同様に、二次元空間の有界領域をGとし、Gの境界上で(x,y)=g(x,y)（与えられた関数）となる関数のうちで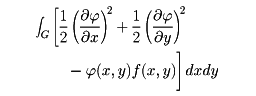

を最小にする(x,y)=u(x,y)を求めよ、という問題は、オイラーの方程式として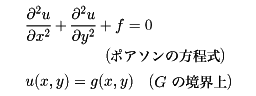

を満足する。

　変分法の問題をオイラーの方程式を用いて解くのも一つの方法であるが、変分法の問題を直接解く直接法もある。とくに、微分方程式をオイラー方程式としてもつ変分問題に直し、変分法の直接法で解くこともよく用いられる。

　直接法で近似解を求めるのにリッツの方法がある。それをポアソンの方程式について説明をすると、境界値として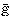(x,y)=g(x,y)となるG上の連続微分可能な関数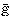(x,y)をとり、u(x,y)=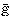(x,y)-w(x,y)と置くと、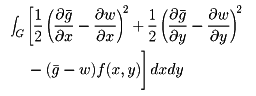

を最小とし、境界上で0となるwを求めればよい。その近似として、境界上で0となる関数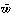₁(x,y),……,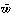_n(x,y)を適当にとり、
　　w_n(x,y)=c₁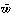₁(x,y)+……+c_n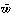n(x,y)
の係数c₁,c₂,……,c_nを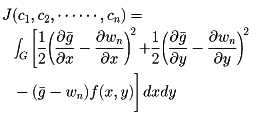

を最小にするように決める。それには、普通の微分法の極値問題より、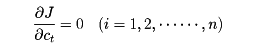

よりc₁、c₂、……、c_nを決めればよい。すなわち、連立一次方程式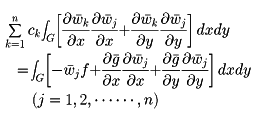

よりc₁、c₂、……、c_nを決めると、近似解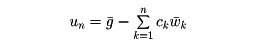

が得られる。

［洲之内治男］

変分法（サイクロイド曲線）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

変分法 (へんぶんほう)
calculus of variations

例えば，垂直な平面内に点P，Qが与えられていて，質点pが重力によってPからQまである曲線に沿って運動するとき，その所要時間を最短にするためにはどのような曲線に沿って動けばよいかという問題を考える。これは1696年にヨハン・ベルヌーイが提起した問題で，数学的には次のように表現される。

　点P，Qを含む垂直平面内に，図のように座標軸をとり，y軸の正の方向が下向きになるようにする。P，Qの座標をそれぞれ（x₀，y₀），（x₁，y₁）とする。質点pが曲線y＝f（x）の上を重力のみによってPからQまで動くとすれば，所要時間Tは，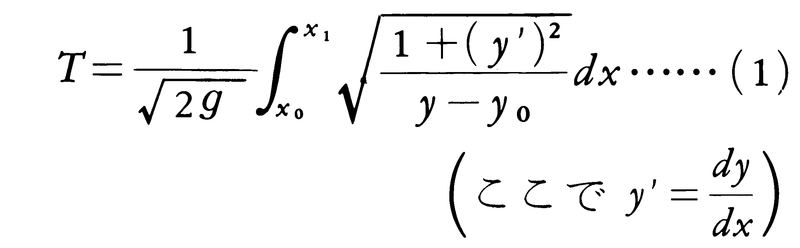

で与えられる。ただしgは重力による加速度である。なお，pが点Pを出発するときの初速度は0としている。問題は，

　y₀＝f（x₀），y₁＝f（x₁）　……（2）　

であるような関数y＝f（x）の中で，（1）のTの値が最小になるものを求めることである。

　問題を一般的に記述すると，ある条件（例えば上記の（2））を満たす関数の集合をΦとすれば，（1）はΦに属する関数y＝f（x）に対して一つの値Tを対応させる式であって，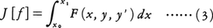

の形をしている。このような“関数の関数”を汎関数といい，与えられた関数の集合Φの中で，ある汎関数の値を最大または最小にする問題を変分法という。初めに述べたベルヌーイの問題が変分法の起りであるが，汎関数functionalという語はJ.アダマールの命名による。

　条件（2）のもとで，（3）を最小にする関数を求める方法は次のとおりである。

η（x）を，

　η（x₀）＝η（x₁）＝0　……（2′）　

を満たす任意の関数とし，εを媒介変数としてY（x;ε）＝y（x）＋εη（x）という形の関数全体を考えてみる。y（x）がJ［・］の値を最小にするならば，εの関数J［Y］はε＝0に対して最小になるから［∂J/∂ε］_ε=0＝0となる。これを（3）に適用し，条件（2′）を使って部分積分を行うと，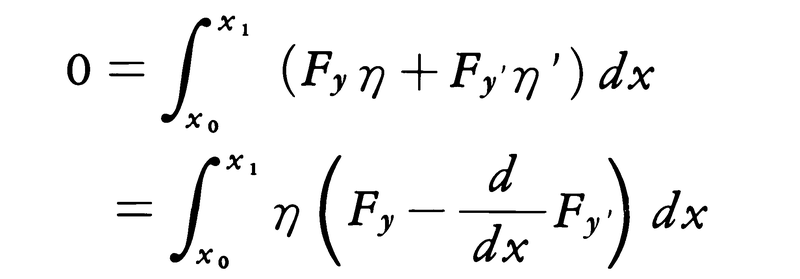

となるから，ηが（2′）を満たす関数の中では任意であることにより，

でなければならない。これをオイラー=ラグランジュの微分方程式，またはオイラーの方程式という。この方程式を満たす関数y（x）のうちで実際に（3）を最小にするものを求めればよい。（4）はJが極値をとるための必要条件であるが，K.ワイヤーシュトラスは十分条件を与えて古典的変分法の理論を完成した。

　近年，変分法にオイラーの方程式を用いない直接法がD.ヒルベルト，R.クーランらによって導入され，解析学の広い範囲にわたる有力な手段にまで発展した。
執筆者：伊藤 清三

図－変分法

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

変分法
へんぶんほう
calculus of variations

たとえば，F を与えられた関数とするとき，積分
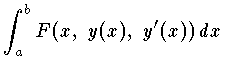の値は，関数 y(x) が指定されるごとに定まる。このように，関数が指定されるごとに1つの値が定まるものを汎関数という。この汎関数の極値問題を論じる数学の分科を変分法，または変分学という。この種の問題は，数学ばかりでなく，物理学にもしばしば現れる。

出典　ブリタニカ国際大百科事典 小項目事典