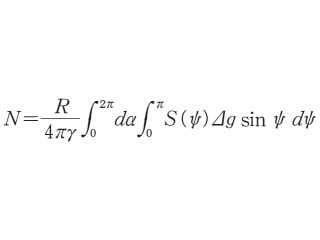ストークス積分（読み）ストークスせきぶん（その他表記）Stokes integral

最新 地学事典

ストークスせきぶん
ストークス積分

Stokes’ integral

地球上の重力異常に重み関数をかけてそれを地球球面にわたり積分してジオイドの高さ（geoidal height）を求めることができるが，この積分をいう。ジオイドの高さは基準楕円体から測る。1849年にG.G.Stokesが導いた。重力異常にかかる重みの関数をストークス関数（Stokes' function）という。この関数はジオイドを計算したい点と重力異常の存在している地点との間の距離の関数で，距離が大きくなるとともに急速に小さくなるので，積分結果は計算点の数百km範囲で大勢が決まる。参考文献：W.A.Heiska- nen et al.（1967） Physical Geodesy, Freeman and Co.

執筆者：藤井 陽一郎

出典　平凡社「最新 地学事典」

法則の辞典

ストークス積分【Stokes integral】

地表重力異常 ⊿&scriptg; からジオイドの高さ N を求める公式．点Pにおけるジオイドの高さは次のようになる．

ここに R は地球の平均半径，γ は平均重力，α は方位角，ψ は原点Oから点PとP′ を見込む角度 ∠POP′ である．

出典　朝倉書店