平均値の定理
へいきんちのていり
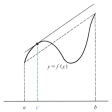
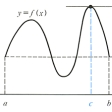
関数f(x)がaとbの間で微分可能であるとき、グラフの上でx=a,x=bに対応する点を結ぶ線分に平行な接線を有する点がaとbの間に少なくとも一つあることを主張する定理(図A)。これは微分積分法における諸定理を導く基礎になる重要な定理である。たとえば、平均値の定理から次の二つの系が帰結できる。〔1〕ある区間で、つねにf′(x)=0ならば、f(x)はこの区間で定数である。〔2〕ある区間で、つねにf′(x)≧0ならば、f(x)はこの区間で単調増加である。
平均値の定理を精密に述べると、次のようになる。関数f(x)が、a≦x≦bで連続、a<x<bで微分可能ならば、a<c<bで、
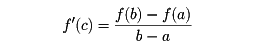
を満たすようなcが存在する。なお、この変形である以下のものも、すべて平均値の定理である。
[竹之内脩]
平均値の定理を証明するためには、普通その特別な場合であるf(a)=f(b)のケースを先に扱う。f(a)=f(b)であるときをロルの定理といい、次のように表される。「関数f(x)がa≦x≦bで連続、a<x<bで微分可能で、f(a)=f(b)であるならば、a<c<bでf′(c)=0を満たすようなcが存在する」(図B)。
[竹之内脩]
「関数f(x)がa≦x≦bで連続、a<x<bで微分可能で、|f′(x)|≦Mであるならば、
a≦x<x′≦bのとき
|f(x′)-f(x)|≦M(x′-x)
である」。これを有限増分の定理という。これは平均値の定理からただちに導かれるものだが、この形では、f(x)がベクトル値関数のときにも適用できる。
[竹之内脩]
「f(x)がa≦x≦bにおいて連続ならば、a≦c≦bで、
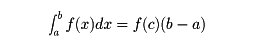
を満たすようなcが存在する」。
[竹之内脩]
「関数f(x),g(x)がa≦x≦bで連続、a<x<bで微分可能であり、かつg′(x)はけっして0にならないものとする。そうすれば、
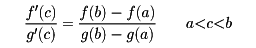
を満たすようなcが存在する」。
[竹之内脩]
二変数の場合について述べる。「f(x,y)が(a,b)のある近傍で偏微分可能ならば、0<θ<1で
f(a+h,b+k)-f(a,b)
=hfx(a+θh,b+θk)
+kfy(a+θh,b+θk)
を満たすようなθが存在する」。ここでfx,fyはそれぞれ偏微分係数を表す。
[竹之内脩]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
平均値の定理 (へいきんちのていり)
mean value theorem
微積分学において有用な定理の一群。
微分法における平均値の定理
(1)関数f(x)がa≦x≦bで連続,a<x<bで微分可能ならば,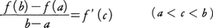 となるcが存在する。
となるcが存在する。
(2)f(x),g(x)が上記(1)のfと同じ仮定を満たし,さらにa<x<bにおいてg′(x)≠0ならば,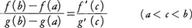 となるcが存在する。(1),(2)をそれぞれラグランジュの平均値定理,コーシーの平均値定理というが,単に平均値定理といえば(1)を指す。(2)でg(x)≡xの場合が(1)であり,(1)でさらにf(b)=f(a)の場合はロルの定理と呼ばれる。
となるcが存在する。(1),(2)をそれぞれラグランジュの平均値定理,コーシーの平均値定理というが,単に平均値定理といえば(1)を指す。(2)でg(x)≡xの場合が(1)であり,(1)でさらにf(b)=f(a)の場合はロルの定理と呼ばれる。
積分法における平均値の定理
(1)a≦x≦bにおいてf(x)は連続であり,またg(x)は積分可能であって符号が一定ならば,
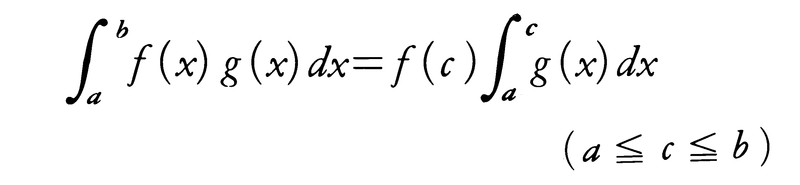
なるcが存在する。
(2)a≦x≦bでf(x)が有界単調でありg(x)が積分可能ならば,

となるcが存在する。(1),(2)をそれぞれ積分法の第1平均値定理,第2平均値定理という。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「平均値の定理」の解説
平均値の定理【theorem of mean value】
区間(a,b)において f(x),&scriptg;(x) が積分可能で,かつ &scriptg;(x) が符号を変えない場合.
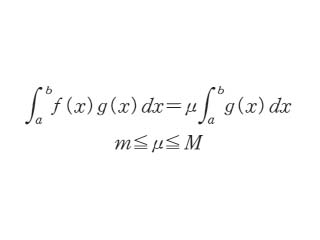
となるような μ が必ず存在する.ただし M,n はこの区間における f(x) の上限値と下限値である.これを積分学の,第一平均値の定理*という.区間(a,b)において f(x),&scriptg;(x) が積分可能で,かつ f(x) が単調なる場合には,
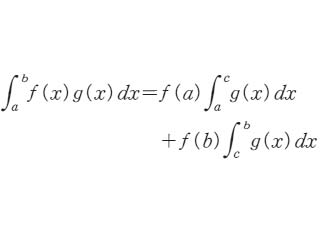
となるような c がその区間内に存在する.これを積分学の第二平均値定理という.
平均値の定理【mean value theorem】
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内の平均値の定理の言及
【微分】より
… 空間を運動する点Pの速度,加速度についても,その座標x,y,zの速度,加速度を用いて上と同様に定義される。
【平均値の定理,テーラーの公式】
関数のグラフを見て考えると,すべての点でf′(x)>0となる関数f(x)は単調増加であることが予想されるが,このような直観的考察は厳密な証明ではない。一般に関数f(x)の増減の状態をその微分係数を用いて調べるとき,次の平均値の定理が重要である。…
※「平均値の定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
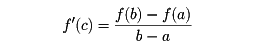
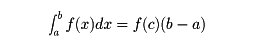
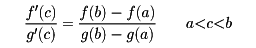


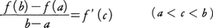 となるcが存在する。
となるcが存在する。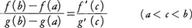 となるcが存在する。(1),(2)をそれぞれラグランジュの平均値定理,
となるcが存在する。(1),(2)をそれぞれラグランジュの平均値定理,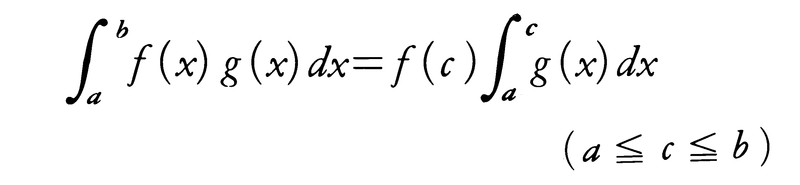

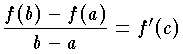 となる c が,区間 [a,b] の
となる c が,区間 [a,b] の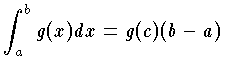 となる c の存在になる。これは,ちょうど c で値をとるとまでいわなくても,m≦g(x)≦M なら
となる c の存在になる。これは,ちょうど c で値をとるとまでいわなくても,m≦g(x)≦M なら 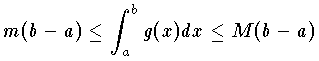 までは簡単で,こうした不等式の形まで含めて平均値の定理ということもある。
までは簡単で,こうした不等式の形まで含めて平均値の定理ということもある。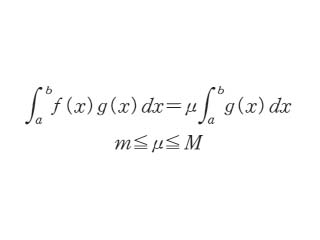
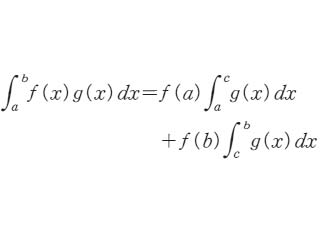
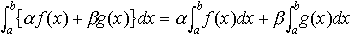 (2)単調性 f(x)≧g(x)ならば,
(2)単調性 f(x)≧g(x)ならば,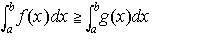 (3)区間に関する加法性 a<c<bならば,
(3)区間に関する加法性 a<c<bならば,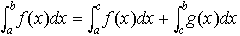 (4)積分の平均値の定理 fが区間[a,b]で連続ならば,
(4)積分の平均値の定理 fが区間[a,b]で連続ならば,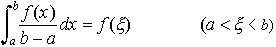 となるξが存在する。 区間に関する加法性(3)がa,b,cの大きさの順に関係なく成り立つようにするため,b≦aのときの積分,
となるξが存在する。 区間に関する加法性(3)がa,b,cの大きさの順に関係なく成り立つようにするため,b≦aのときの積分,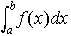 を次のように定める。…
を次のように定める。…