ブリタニカ国際大百科事典 小項目事典 「ダルブーの定理」の意味・わかりやすい解説
ダルブーの定理
ダルブーのていり
Darboux's theorem
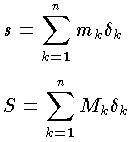 は,それぞれ確定した極限値 l ,L に近づく。また l と L の間には l≦L なる関係が成り立つ。これは,極限の記法によって
は,それぞれ確定した極限値 l ,L に近づく。また l と L の間には l≦L なる関係が成り立つ。これは,極限の記法によって 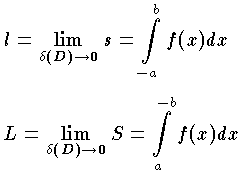 と表わすことができる。 l=L のときが,リーマン積分可能な場合にあたる。
と表わすことができる。 l=L のときが,リーマン積分可能な場合にあたる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報

