テーラー展開
てーらーてんかい
関数f(x)がx=aの近傍で定義され、そこでn回微分可能であるならば、f(x)は、
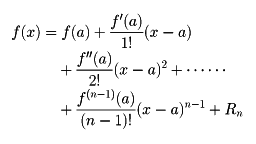
と表される。これをテーラーの定理といい、関数をこの形に書き表すことをテーラー展開という。ここでRnは剰余項といい、次のいろいろな形の表し方がある。以下でξはaとxの間のある数を表す。
(1)ラグランジュの剰余項
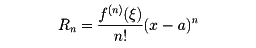
(2)コーシーの剰余項
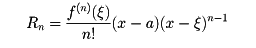
(3)シュレーミルヒの剰余項
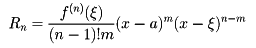
ここでmは、1≦m≦nを満たす自然数とする。
(4)積分形
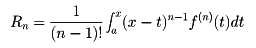
B・テーラーはこれを1715年に発表した。それはもちろんこのような精密な形ではなかったが、18世紀末から19世紀にかけて、いろいろな数学者によりその形が整えられた。また、とくにa=0の特別な場合をマクローリン展開という。n=1の場合は、別項に述べる「平均値の定理」となる。
aの近傍でf(x)が無限回微分可能で、
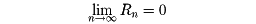
がどのxについてもいえるならば、
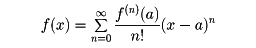
という無限級数に表すことができることになる。これをテーラー級数という。テーラー級数に展開することをテーラー展開ということもある。
[竹之内脩]
たとえば、二変数のときは次の形になる。
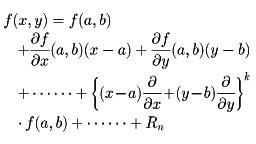
ただし、
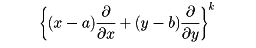
は、この式を二項定理によって展開して、
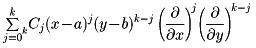
としたのち、
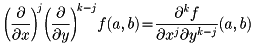
とすることを意味する。剰余項についてはここでは省略する。
[竹之内脩]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
世界大百科事典(旧版)内のテーラー展開の言及
【テーラー級数】より
…すなわちf(x)は区間Iで(1)のテーラー級数に展開される。このとき(1)をf(x)の(区間Iにおけるaを中心とする)テーラー展開という。テーラー級数(1)において,とくにa=0の場合をマクローリン級数といい,f(x)が0を中心としてこの形の級数に展開されるとき,その展開をマクローリン展開という。…
【微分】より
…また,aのある近傍で一様に,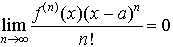 となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,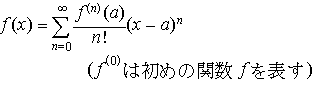 が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を
が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を[テーラー級数]という。
【微分】
関数y=f(x)がx=aにおいて微分可能ならば,xのaからの変化⊿x→0のとき⊿y/⊿x→f′(a)であるから, (⊿y/⊿x)-f′(a)=εとおけば, ⊿y=f′(a)⊿x+ε・⊿x ……(14) ⊿x→0のときε→0 ……(15) となる。…
※「テーラー展開」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
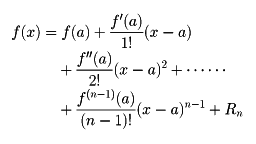
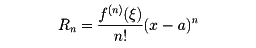
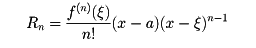
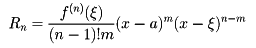
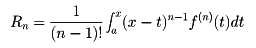
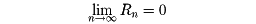
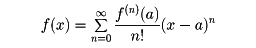

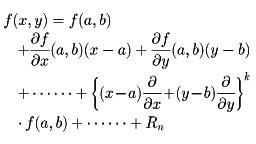
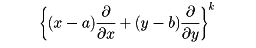
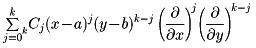
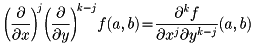

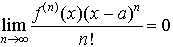 となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,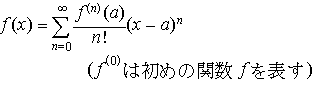 が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を
が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を