改訂新版 世界大百科事典 「テーラー級数」の意味・わかりやすい解説
テーラー級数 (テーラーきゅうすう)
Taylor series
実変数xの関数f(x)がx=aにおいて何回でも微分可能なとき,級数,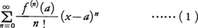
をf(x)のaを中心とするテーラー級数という。テーラー級数が収束するxの範囲,および収束するときにそれが関数f(x)に等しくなるかどうかが問題となる。まずRを,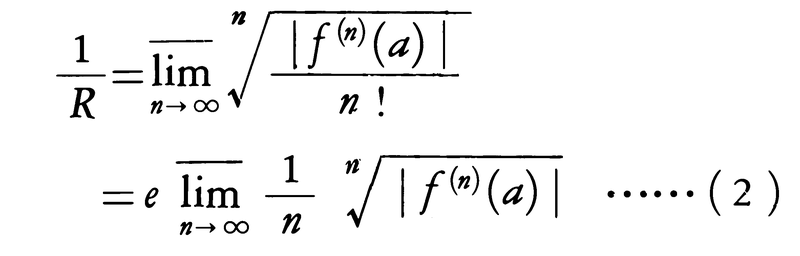
によって定義する(ただし,この上極限が0のときはR=∞,上極限が∞のときはR=0とする)。このとき,|x|<Rならば級数(1)は収束するが,それがf(x)を表すとは限らない。f(x)がaを内部に含むある区間Iで何回でも微分可能ならば,その区間の中のxに対して次のように表される。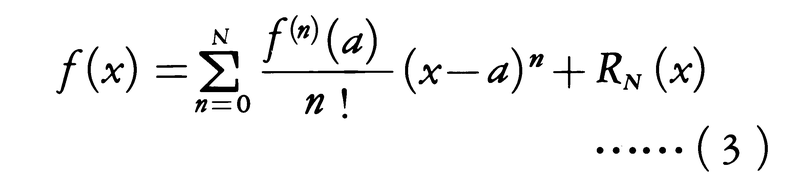
ここでRn(x)は剰余項と呼ばれ,各種の形に表されるが,もっとも簡単なものは下記のラグランジュの剰余形式である。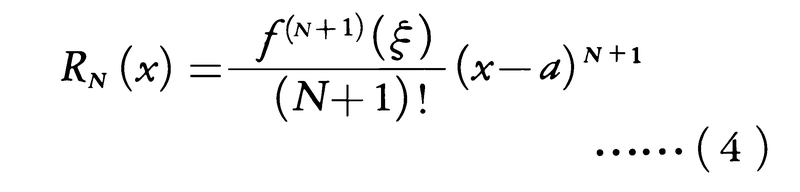
ただし,ξはaとxとの間にある適当な数であって,a,x,Nに関係して定まるものである。N→∞のとき区間Iの任意の点xにおいてRn(x)→0となるならば,この区間で無限級数(1)はf(x)を表す。すなわちf(x)は区間Iで(1)のテーラー級数に展開される。このとき(1)をf(x)の(区間Iにおけるaを中心とする)テーラー展開という。テーラー級数(1)において,とくにa=0の場合をマクローリン級数といい,f(x)が0を中心としてこの形の級数に展開されるとき,その展開をマクローリン展開という。
f(x)がある区間で無限回微分可能であっても,テーラー展開されるとは限らない。例えば,関数,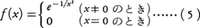
はすべての実数xにおいて無限回微分可能であり,x=0においてはf⁽n⁾(0)=0(n=0,1,2,……)となるから,テーラー級数(1)においてa=0とするとすべての項が0となるが,x≠0ならばf(x)≠0であるから,f(x)を0を中心としてテーラー展開することはできない。
テーラー展開の例。実数α≠0に対して,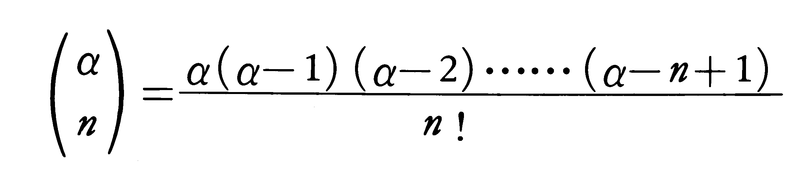
とする(αがn以上の自然数Nのときは,これは組合せの数nCnである)。このとき,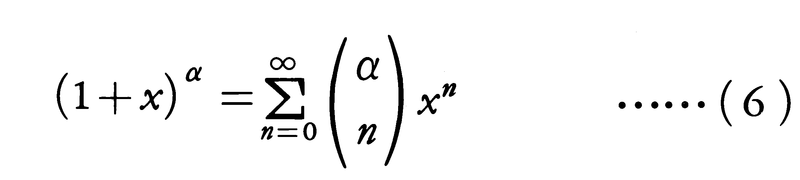
ただし,一般には-1<x<1で収束,α>0ならば-1≦x≦1で収束し,-1<α<0ならば-1<x≦1で収束する。とくにαが自然数ならば(6)の右辺は有限個の項からなり,(6)はすべての実数xに対して成立する。これはふつうの二項定理にほかならない。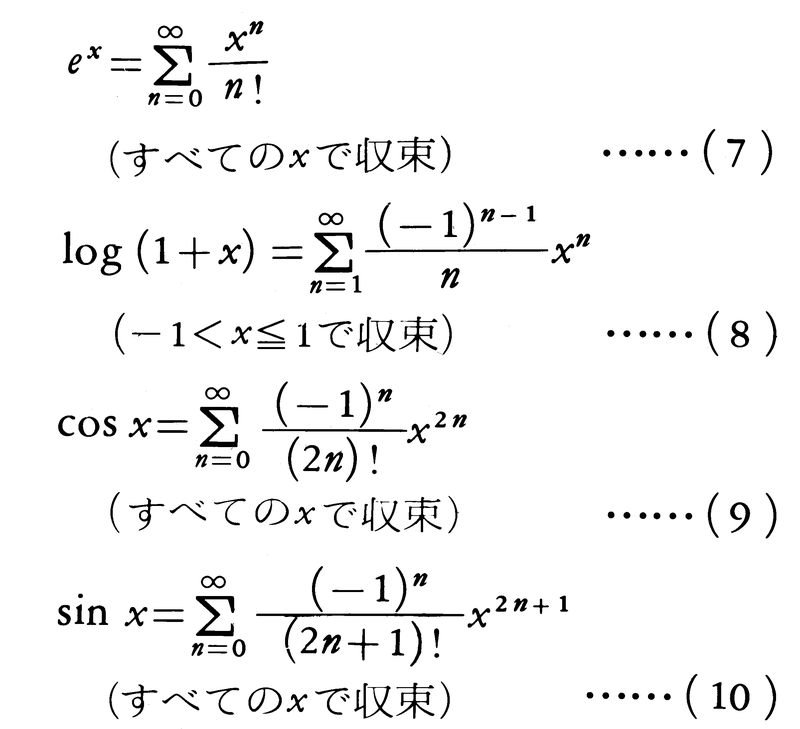
f(x)がx=aを含む区間で(N+1)回まで微分可能ならば,その区間で,このNに対して(3),(4)が成立する。この事実をテーラーの定理という。
複素変数の場合。変数が複素数zの関数f(z)があって,z=a(複素数)の近傍で正則ならば,Rを(2)によって定義するとき,f(z)は|z-a|<Rにおいて(1)と同じ形の級数に展開される。すなわち,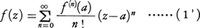
これも(1)と同様にテーラー級数といい,この展開式を複素関数f(z)のテーラー展開という。前に例にあげた(6)~(10)における実変数xをすべて複素変数zに書き換えることができる。ただし,(6),(8)は|z|<1において収束し,(7),(9),(10)はすべての複素数zに対して収束する。
→解析関数 →級数 →冪(べき)級数
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


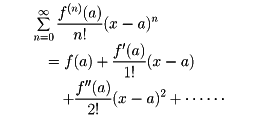


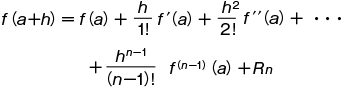 ただしこの級数は,上式の右辺の剰余項 Rn=f(n)(a+θh)hn/n! が n→∞ のとき0に収束するようなすべての x の値について成立する。上の級数を,f(x) を展開して得られるテーラーの級数という。
ただしこの級数は,上式の右辺の剰余項 Rn=f(n)(a+θh)hn/n! が n→∞ のとき0に収束するようなすべての x の値について成立する。上の級数を,f(x) を展開して得られるテーラーの級数という。
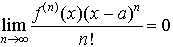 となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,
となるときは,その近傍の中の任意のxに対して,(11)でn→∞とした式,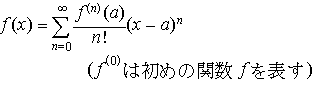 が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を
が成立する。この式をf(x)のテーラー展開といい,右辺の無限級数を