台形公式（読み）だいけいこうしき（その他表記）trapezoidal rule

改訂新版　世界大百科事典

台形公式 (だいけいこうしき)
trapezoidal rule

定積分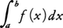の近似計算のための公式。区間［a，b］をn等分した分点をa＝x₀，x₁，x₂，……，x_n＝bとし，それらに対応するf（x）の値をy₀，y₁，y₂，……，y_nとする。n個の小区間［x₀，x₁］，［x₁，x₂］，……，［x_n-1，x_n］において，関数y＝f（x）のグラフを，それぞれ図のように線分で置き換えて

　h＝\(\frac{b－a}{n}\)

とすると，各小区間における積分の近似値は，台形の面積の公式により，それぞれ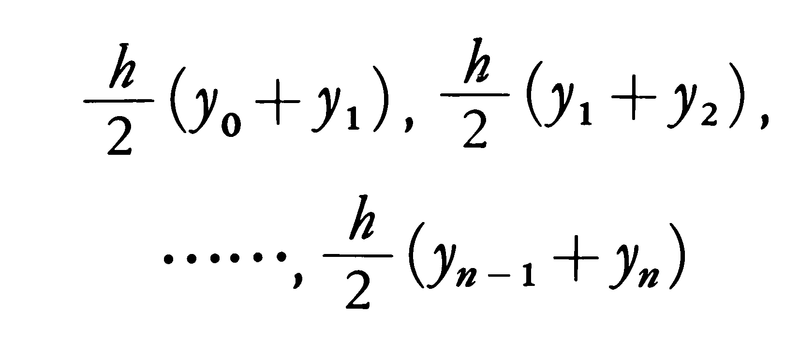

となるから，これらを加えて次の近似公式が得られる。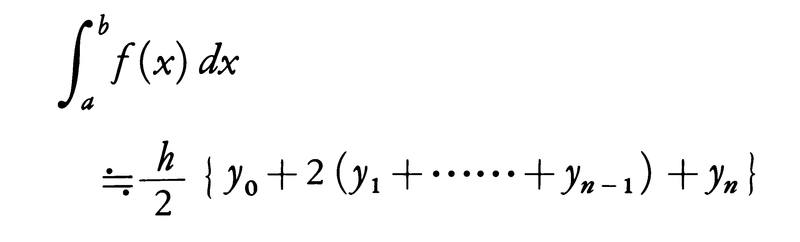

これを台形公式という。台形公式はシンプソンの公式より精度は悪いが，近年はコンピューターの発達により，分割数nを大きくすることによって精度をあげることができるので，式の形が簡単な台形公式も有用である。
執筆者：伊藤 清三

図－台形公式

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

台形公式
だいけいこうしき
trapezoidal formula

台形則ともいう。定積分の近似値を求める公式の一つ。定積分の近似値を計算するとき，区間 [a ，b] を n＋1 個の分点 x₀ ，x₁ ，x₂ ，…，x_n (ただし a＝x₀＜x₁＜x₂＜…＜x_n-1＜x_n＝b ) で n 個の小区間に等分し，各分点 x_i ( i＝0 ，1，2，…，n ) に対する f(x) の値 f(x_i) を計算し，次の公式に代入する。
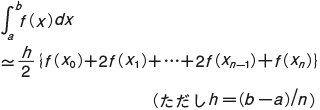上の公式は定積分の近似値を台形の和として求めるので，台形公式という。これはニュートン＝コーツの公式の n＝1 の場合にあたる。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の台形公式の言及

【数値積分】より

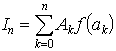…このときIの近似，における重みは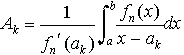，である。とくにn＝1のときが台形公式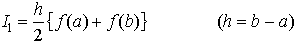，n＝2のときがシンプソンの1/3公式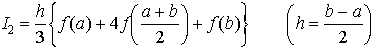，n＝3のときがシンプソンの3/8公式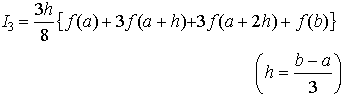，である。よりよい近似を得るため，実際は[a,b]を多くの小区間に等分し，各小区間でn次多項式f_n(x)を用いる複合則を適用する。…

※「台形公式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」